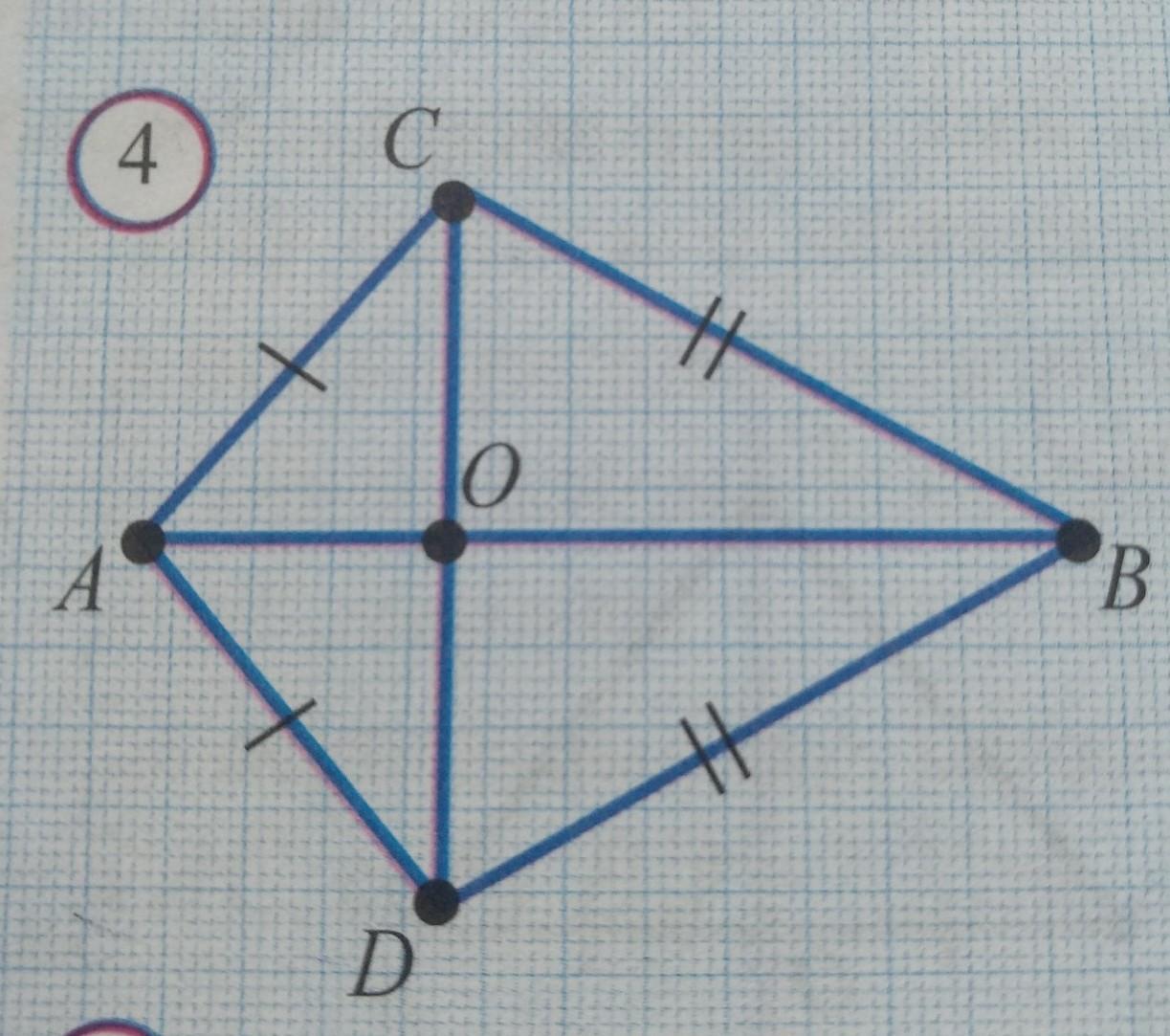
на рисунке 4: а) ∆ABC=∆ABD; б)∆BOC=∆BOD в)∆AOC=∆ABD Докажите,что AB перпендекулярны
CD
Ответы
В равенстве в) опечатка: для того, чтобы задача была корректной, должно быть ∆AOC=∆AОD.
Две прямые перпендикулярны, если по крайней мере один угол между ними равен 90°.
а) Пусть ∆ABC=∆ABD.
Так как эти треугольники равны, то ∠CAB = ∠DAB. Это значит, что АО — биссектриса ∠DAC (так как делит угол, из которого проведена, пополам).
Рассмотрим ∆ADC. На рисунке видим две равные стороны AC и AD, значит, он равнобедренный с основанием DC.
Биссектриса равнобедренного треугольника, проведенная к основанию, является также высотой (перпендикуляром к стороне).
Значит, АО ⊥ DC и ∠AOD = ∠AOC = 90°.
Поэтому AB ⊥ CD.
б) Пусть ∆BOC=∆BOD
Рассмотрим ∆BCD. На рисунке видим две равные стороны BC и BD, значит, он равнобедренный с основанием DC.
Рассмотрим ∆BOC и ∆BOD. По условию, это равные треугольники. Значит, DO = OC.
Отсюда, ВО — это медиана (так как делит сторону, к которой проведена, пополам).
Медиана равнобедренного треугольника, проведенная к основанию, является также высотой (перпендикуляром к стороне).
Значит, BО ⊥ DC и ∠BOD = ∠BOC = 90°.
Поэтому AB ⊥ CD.
в) Пусть ∆AOC=∆AОD
Рассмотрим ∆ADC. AD = AC, значит, он равнобедренный с основанием DC.
Рассмотрим ∆AOC и ∆AОD. По условию, это равные треугольники. Значит, DO = OC.
Отсюда, АО — это медиана.
Медиана равнобедренного треугольника, проведенная к основанию, является также высотой (перпендикуляром к стороне).
Значит, АО ⊥ DC и ∠AOD = ∠AOC = 90°.
Поэтому AB ⊥ CD.