Предмет: Алгебра,
автор: Tolikvvv
ПОМОГИТЕ НАЙТИ ПРОИЗВОДНЫЕ (КРОМЕ ПЕРВЫХ ДВУХ) все что сможете сами решить
Приложения:
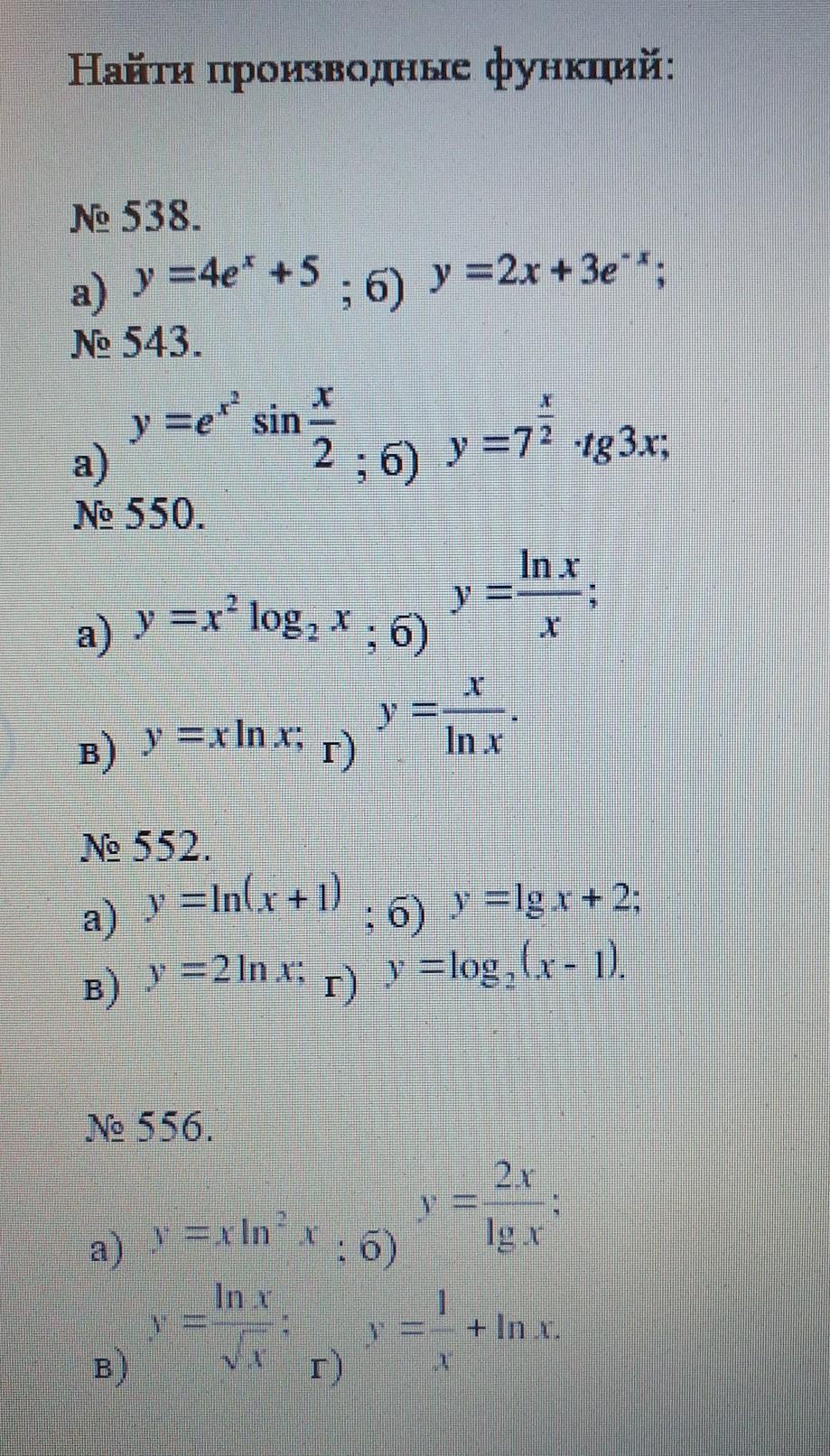
Ответы
Автор ответа:
1
543
а)
б)
550
а)
б)
в)
г)
552
а)
б)
в)
г)
556
а)
б)
в)
г)
Tolikvvv:
спасибо огромное
Похожие вопросы
Предмет: Биология,
автор: ulanova201653
Предмет: Русский язык,
автор: Марусяяяооо
Предмет: Математика,
автор: vertovmax
Предмет: Математика,
автор: ника2773