Question

Даю 20 балів
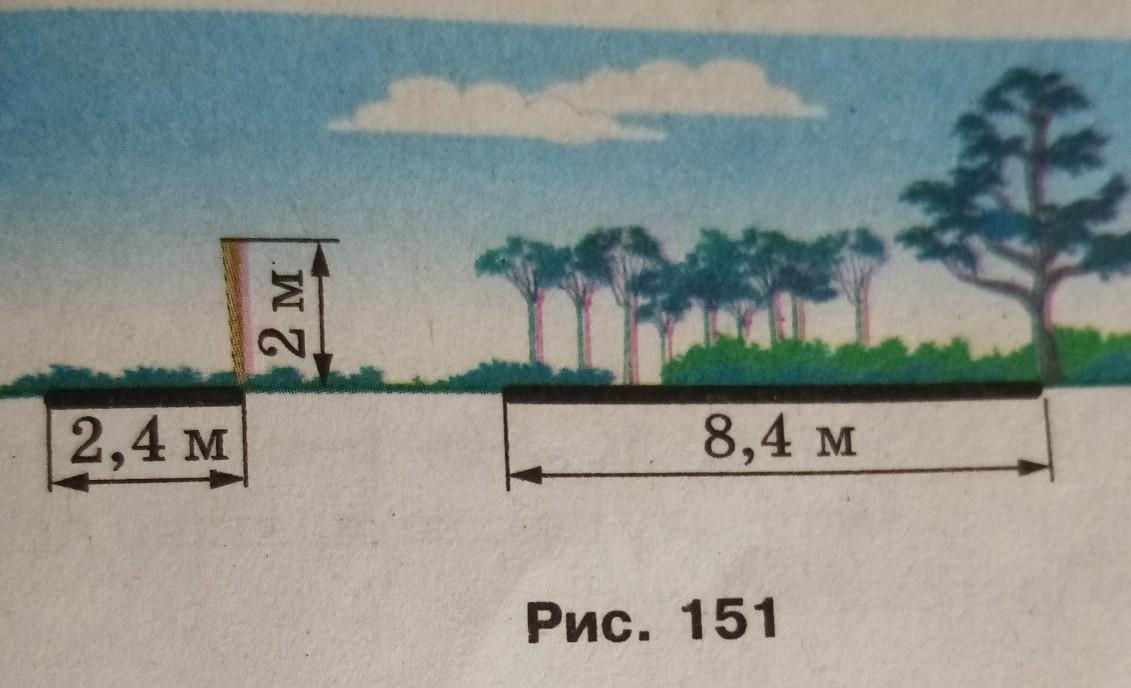
Знайдіть висоту дерева, якщо довжина його тіні дорівнює
8,4 м, а довжина тіні від вертикального стовпа заввишки
2 му той самий час доби дорівнює 2,4 м (рис. 151).​

Answer 1

Ответ:

7 м

Объяснение:

• Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны (1 признак подобия треугольников).

ΔBAC подобен ΔNAK :

1. ∠BAC = ∠NAK - как общий ( т.к. угол падения солнечных лучей в одном и том же месте, в одно и тоже время суток одинаковый),
2. NK⊥AC, BC⊥AC - как высоты столба и дерева соответственно ⇒ ∠NKA=∠BCA=90°

Из подобия треугольников следует, что их соответственные стороны пропорциональны:

$\frac{BC}{NK} =\frac{AC}{AK}$

$\frac{BC}{2} =\frac{8,4}{2,4}$

$BC = \frac{8,4*2}{2,4} = 7$

Высота Дерева - 7 м