Предмет: Алгебра,
автор: Аноним
помогите, пожалуйста!!!
Приложения:
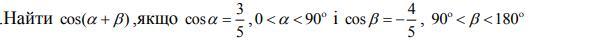
Ответы
Автор ответа:
1
Дано:
Найти:
Решение.
1)
2)
3) Воспользуемся формулой косинуса суммы двух углов:
Ответ:
https://znanija.com/task/41150648
Похожие вопросы
Предмет: Физика,
автор: Veteg
Предмет: Математика,
автор: ivanmakarov200
Предмет: Математика,
автор: sledak73567
Предмет: Математика,
автор: ArtemSkill1
можешь, пожалуйста помочь еще?