Предмет: Математика,
автор: averaxina2016
Срочно нужна помощь с дифференциальным уравнением!!!
Приложения:
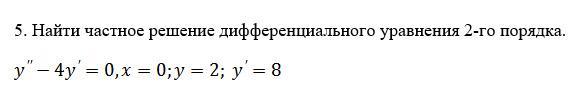
Ответы
Автор ответа:
1
Ответ:
замена:
общее решение
частное решение
averaxina2016:
выручили)
Похожие вопросы
Предмет: Математика,
автор: KarimovaElvira
Предмет: Биология,
автор: MrClicky
Предмет: Українська мова,
автор: гном1
Предмет: Химия,
автор: alialameen83p0uu0w
Предмет: Геометрия,
автор: tadashio