Предмет: Алгебра,
автор: Нпои
вычислить определенный интеграл
Приложения:
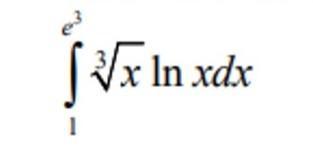
Ответы
Автор ответа:
1
Ответ:
По частям:
формула:
подставляем пределы:
Похожие вопросы
Предмет: Алгебра,
автор: Elizabethpride
Предмет: Английский язык,
автор: Leonov3viktor
Предмет: Физика,
автор: 4444tolik
Предмет: Математика,
автор: АнастасияСа
Предмет: Физика,
автор: vicandrukh