Тело брошено горизонтально со скоростью v0. Через 2 сек скорость составила 30 м/с. Найти высоту с которой было брошено тело и начальную скорость, если известно, что тело упало через 4 сек. Найти скорость в момент падения.
Ответы
Дано:
t1 = 2 с
t2 (через которое упало на поверхность) = 4 с
v1 = 30 м/с
g = 10 м/с^2
Найти:
v0 - ?
h = ?
v2 (в момент падения) - ?
Вывод формул и объяснение:
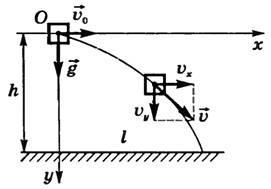
Начало точки координат на рисунке (прикреплённый файл) нужно совместить с точкой начального положения тела. По данному рисунку видно, что горизонтальная скорость , а сам x (горизонтальное смещение) в таком случае равен
, так как горизонтальная скорость неизменна (тело движется равномерно, т.к. мы пренебрегаем сопротивлением воздуха).
Вертикальная скорость же равноускоренная (тело движется без начальной вертикальной скорости и подвержено силе притяжения) и равна , а y (вертикальное смещение) -
. Так мы можем определить высоту, зная время, через которое тело упало на поверхность (t2) :
.
,
Зная и
можем узнать
по теореме Пифагора:
. Подставляем уже выведенные формулы
и
и получаем:
Решение:
м
Так как нам известна скорость через 2 секунды, то мы можем вывести начальную скорость:
м/с Выводим из этой формулы
м/с ≈ 22.36 м/с
Теперь находим скорость в момент падения:
м/с ≈ 45.83 м/с
Ответ:
- h = 80 м
= 22.36 м/с
= 45.83 м/с