Предмет: Геометрия,
автор: idel121206
Sangers пожалуйста помоги пожалуйста!❤
Приложения:
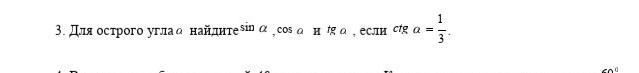
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Котангенс острого угла больше нуля. ⇒
idel121206:
Большое спасибо вам!)))❤
Удачи.
Здравствуйте! Пожалуйста ответьте на мой последний вопрос он по математике. Если вам не трудно. Я за него дам 50 баллов. sangers1959 помогите и мне пожалуйста
Похожие вопросы
Предмет: Литература,
автор: didar76
Предмет: Математика,
автор: vitas1337q
Предмет: Математика,
автор: NatashkaP37
Предмет: Биология,
автор: Анастасияплюс
Предмет: Химия,
автор: nathanbeezy