Предмет: Алгебра,
автор: Lilipum
Вычислить производную функции:
Приложения:
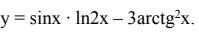
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Химия,
автор: МАЛИНА09
Предмет: Русский язык,
автор: lovalovatt
Предмет: Геометрия,
автор: ypotapova2016
Предмет: Математика,
автор: RSL1
Предмет: Математика,
автор: kamika334