Question

решите...что-то совсем не получается только не через косинус...мы еще это не проходили

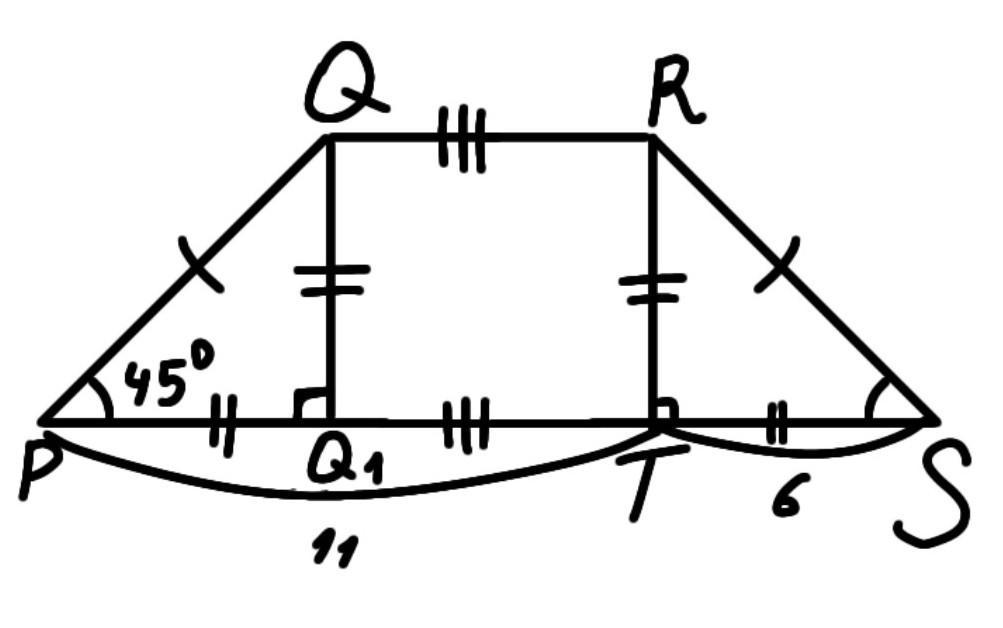
В равнобедренной трапеции PQRS угол Р равен 45°. RT-высота, РТ=11 см, ТS=6см. Найдите площадь трапеции.

Answer 1

Площадь трапеции:

$s = \frac{a + b}{2} \times h$

1)Т.к. трапеция равнобедренная => угол Р = углу S = 45°

2)Рассмотрим ∆RTS

RT - высота => ∆ прямоугольный

Угол SRT = 90° - угол RST = 90° - 45° = 45°

Из этого делаем вывод,что ∆RTS - равнобедренный и ST = RT = 6

3) ∆RTS = ∆ QQ1Р

По двум углам (угол QРQ1 = углу RST,угол PQQ1 = углу SRT) и прилежащей к ним стороне(PQ=RS по условию)

Из этого следует,что PQ1 = 6

4) QR = Q1T = PT - PQ1

QR = 11-6 = 5

5) PS = PT + TS

PS = 11+6 = 17

6)

$S = \frac{5 + 17}{2} \times 6 = 11 \times 6 = 66$ см²

Ответ: площадь трапеции равна 66 см²