Question

Найдите область определениях функции f(x)=x-4/x^2-x-6

Answer 1

Сначала интересная теория:

Область определения D(f) функции f(x) - это все те значения "x", которые можно подставить в функцию. И при этом она будет иметь смысл, то есть вычисляться.

В данном примере - функция дробная. Значит, знаменатель не должен равняться нулю. Решаем:

Решение:

$\mathtt{f(x)=\dfrac{x-4}{x^2-x-6}} \\ \\ \\\mathtt{D(f): x^2-x-6 \neq 0}$

Составим и решим уравнение:

$\mathtt{x^2-x-6=0} \\ \\ \mathtt{D=b^4-4ac=(-1)^2-4\cdot1\cdot(-6) = 1+24 = 25 = 5^2}} \\ \\ \mathtt{x_1=\dfrac{1+5}{2\cdot1} = 3;} \ \ \ \mathtt{x_2 = \dfrac{1-5}{2} = -2}$

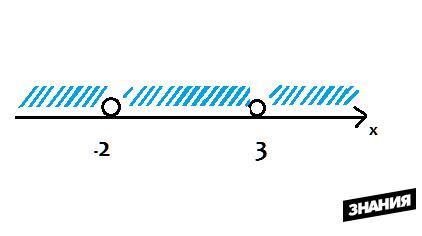
теперь чертим числовую прямую и отмечаем область значений, картинка в приложении. Точки -2, 3 выколотые, так как их нельзя подставлять в функцию: при них знаменатель обращается в ноль

D(f) = (-∞;-2)⋃(-2;3)⋃(3;+∞)

Ответ: D(f) = (-∞;-2)⋃(-2;3)⋃(3;+∞)