Предмет: Геометрия,
автор: wonhord
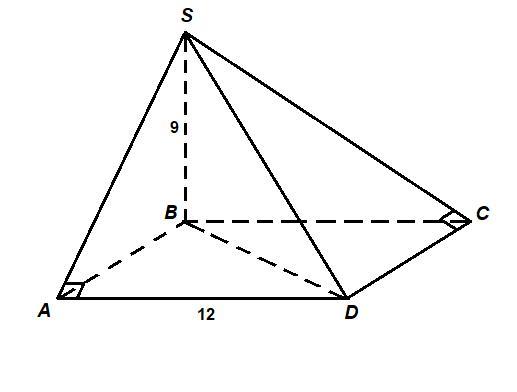
Основою піраміди є квадрат зі стороною 12 см Одне бічне ребро перпендикулярно площині основи і дорівнює 9 см. Обчислити прощу бічної поверхні.
Ответы
Автор ответа:
1
Ответ:
288 см²
Объяснение:
ΔSBA = ΔSBC по двум катетам (SB - общий, ВА = ВС как стороны квадрата).
см²
Из прямоугольного треугольника SBA по теореме Пифагора:
см
BA⊥AD как стороны квадрата,
ВА - проекция SA на плоскость основания, значит
SA⊥AD по теореме о трех перпендикулярах.
Аналогично, SC⊥CD.
ΔSAD = ΔSCD по гипотенузе и катету (AD = DC как стороны квадрата, SD - общая).
см²
Площадь боковой поверхности равна сумме площадей боковых граней:
Sбок. = 54 · 2 + 90 · 2 = 108 + 180 = 288 см²
Приложения:
Похожие вопросы
Предмет: Математика,
автор: seefs
Предмет: Математика,
автор: kopylovasofiy
Предмет: Математика,
автор: bossik1319
Предмет: Физика,
автор: danillbiz
Предмет: Математика,
автор: egorik2506