Question

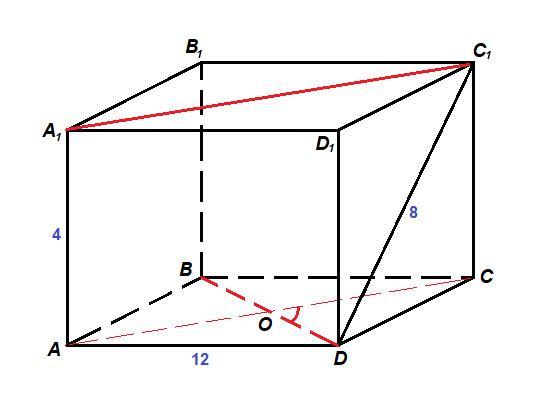
Дано прямокутний паралелепіпед ABCDA1B1C1D1. Знайти кут між прямими A1С1 і BD, якщо AD = 12 см, С1D = 8 см, AA1 = 4 см. Будь ласка, дуже потрібна допомога!!!

Answer 1

Ответ:

∠(A₁C₁; BD) = 60°

Объяснение:

Прямые А₁С₁ и BD - скрещивающиеся.

АС║А₁С₁, значит ∠(АС; BD) = ∠(A₁C₁; BD) = ∠COD.

ΔC₁CD:  ∠C₁CD = 90°, CC₁ = AA₁ = 4 см, по теореме Пифагора

  $CD=\sqrt{C_1D^2-CC_1^2}=\sqrt{8^2-4^2}=\sqrt{64-16}=\sqrt{48}=4\sqrt{3}$ см

ΔACD: ∠ADC = 90°, по теореме Пифагора

 $AC=\sqrt{AD^2+CD^2}=\sqrt{12^2+(4\sqrt{3})^2}=$

$=\sqrt{144+48}=\sqrt{192}=8\sqrt{3}$  см

• Диагонали прямоугольника равны и точкой пересечения делятся пополам:

$OC=OD=\dfrac{1}{2}AC=4\sqrt{3}$  см

Значит, ΔCOD равносторонний, ∠COD = 60°.