Предмет: Геометрия,
автор: 30112006edik
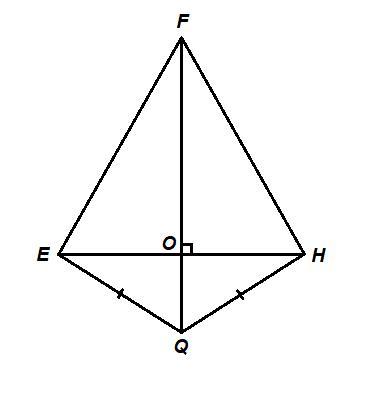
В четырехугольнике E F H Q EQ=QH, E H пересекает FQ под прямым углом. Докажи, что треугольники F E Q и F Q H равны.
Ответы
Автор ответа:
7
Ответ:
EQ = QH по условию, значит
ΔEQH - равнобедренный.
QO - высота равнобедренного треугольника, значит QO и биссектриса,
∠EQO = ∠HQO.
В треугольниках FEQ и FHQ:
- EQ = QH по условию,
- ∠EQF = ∠HQF (доказано выше),
- FQ - общая сторона, следовательно
ΔFEQ = ΔFHQ по двум сторонам и углу между ними.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: jgthtnnf
Предмет: Математика,
автор: Пирожо4ек
Предмет: Математика,
автор: kliza00
Предмет: Алгебра,
автор: kotalina32
Предмет: Математика,
автор: danik177