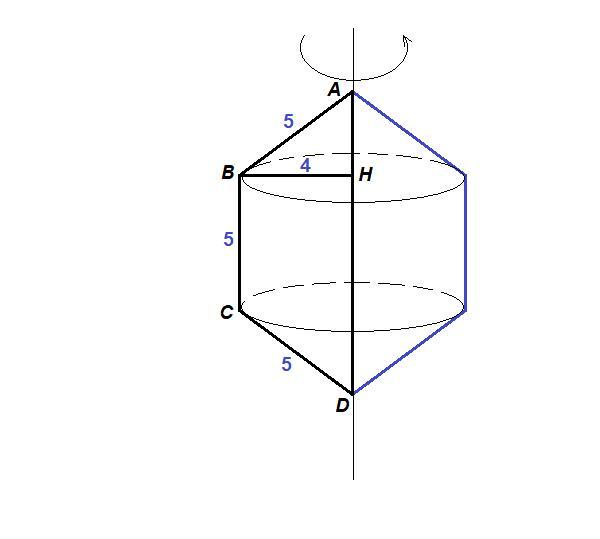
Рівнобедрена трапеція, бічні сторони та менша основа якої дорівнюють по 5 см, обертається навколо більшої основи. Знайдіть площу поверхні утвореного тіла, якщо висота трапеціїї дорівнює 4 см.
Ответы
Равнобедренная трапеция, боковые стороны и меньшее основание которой равны по 5 см, вращается вокруг большего основания.
Найдите площадь поверхности полученного тела, если высота трапеции равна 4 см.
Ответ:
80π см²
Объяснение:
При вращении равнобедренной трапеции вокруг большего основания получается тело, состоящее из цилиндра и двух равных конусов.
Радиусы оснований цилиндра и конусов равны, и равны высоте трапеции: R = ВН = 4 см.
Образующая цилиндра (или его высота) - меньшее основание трапеции: h = ВС = 5 см.
Образующая конуса - боковая сторона трапеции: l = АВ = CD = 5 см.
Поверхность тела состоит из боковой поверхности цилиндра и двух боковых поверхностей конуса.
Площадь боковой поверхности цилиндра:
Sбок.ц. = 2πRh = 2π · 4 · 5 = 40π см²
Площадь боковой поверхности конуса:
Sбок. к. = πRl = π · 4 · 5 = 20π см²
Площадь поверхности полученного тела:
S = Sбок.ц. + 2Sбок.к = 40π + 2 · 20π = 80π см²