Предмет: Алгебра,
автор: pashagutorov00
Варианте найти общий интеграл дифференциального уравнения:
Приложения:
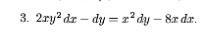
Ответы
Автор ответа:
1
Ответ:
общее решение
Похожие вопросы
Предмет: Алгебра,
автор: dianamineeva
Предмет: Русский язык,
автор: detkalove
Предмет: Українська література,
автор: lukasya5
Предмет: Математика,
автор: Alii01