Предмет: Геометрия,
автор: valeevyura
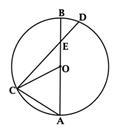
АВ – диаметр окружности с центром O, который пересекает хорду CD в точке E, лежащей на BO. Градусная мера дуги AC равна 60∘, OE=0,6⋅OA. Найдите 7⋅cos∠CEA
Приложения:
Ответы
Автор ответа:
2
OA=OB=OC (радиусы)
Пусть OA=10
OE =0,6 OA =6
∠AOC =∪AC =60° (центральный угол)
△AOC - равносторонний (равнобедренный с углом 60°)
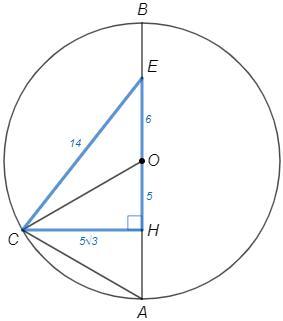
Опустим высоту CH.
В равностороннем треугольнике высота является медианой.
OH =OA/2 =5
EH =5+6 =11
CH =OH tg60° =5√3
CE =√(CH^2 +EH^2) =14 (т Пифагора)
cos(CEH) =EH/CE =11/14
Ответ: 7cos(CEA) =11/2
Приложения:
Похожие вопросы
Предмет: Физика,
автор: kurunov1
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: mirabeylice738
Предмет: Математика,
автор: АдылжанНиязов1
Предмет: Алгебра,
автор: mashyla295ovebte