Сформулируйте и докажите теорему об углах с соответственно параллельными сторонами
Ответы
Ответ:
Углы с соответственно параллельными сторонами равны, если они одновременно острые или одновременно тупые, или в сумме составляют 180°, если один из них острый, а другой тупой.
1) Дано:
∠ВАС - острый,
∠КМЕ - острый,
АВ║МК, АС║МЕ.
Доказать: ∠ВАС = ∠КМЕ.
Доказательство:
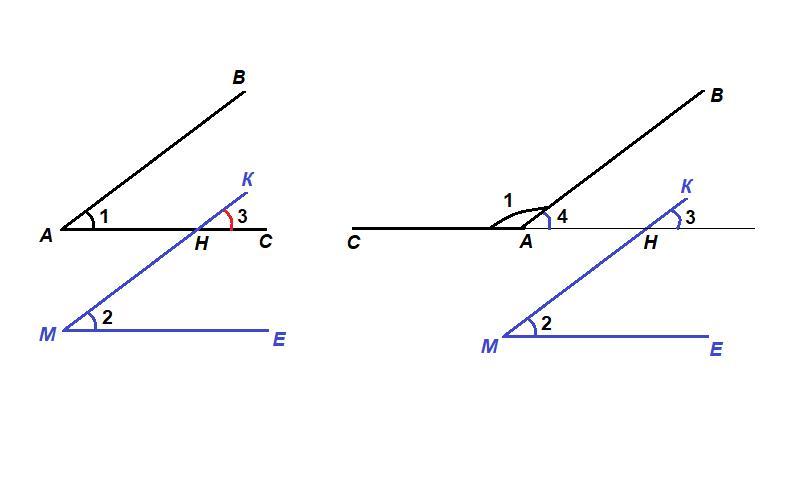
Продлим стороны углов до пересечения в точке Н (см. рисунок).
∠1 = ∠3 как соответственные при пересечении АВ║МК секущей АС,
∠2 = ∠3 как соответственные при пересечении АС║МЕ секущей МК, значит
∠1 = ∠2, т.е. ∠ВАС = ∠КМЕ.
2) Дано:
∠ВАС - тупой,
∠КМЕ - острый,
АВ║МК, АС║МЕ.
Доказать: ∠ВАС + ∠КМЕ = 180°.
Доказательство:
Продлим стороны углов до пересечения в точке Н (см. рисунок).
∠4 = ∠3 как соответственные при пересечении АВ║МК секущей АС,
∠2 = ∠3 как соответственные при пересечении АС║МЕ секущей МК, значит
∠4 = ∠2.
∠1 + ∠4 = 180° (смежные углы), значит ∠1 + ∠2 = 180°, т.е.
∠ВАС + ∠КМЕ = 180°