Предмет: Алгебра,
автор: pashagutorov00
Варианте найти общий интеграл дифференциального уравнения:
Приложения:
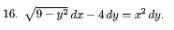
Ответы
Автор ответа:
1
Ответ:
общее решение
Похожие вопросы
Предмет: Математика,
автор: diana20018
Предмет: Математика,
автор: NastyaP1
Предмет: Биология,
автор: 07а
Предмет: Музыка,
автор: LisaKissen