Предмет: Геометрия,
автор: okssuhowa
Даны А(1;3;7); В(2;4;1) и вектор а{2;3;1}. Вычислить косинус угла между векторами АВ и а.
Ответы
Автор ответа:
1
Ответ:
cos ∠ (AB, a) = -1 / (2√133)
Объяснение:
Вектор AB {2 - 1; 4 - 3; 1 - 7} = {1; 1; -6}
Вектор a {2; 3; 1} - по условию
Их скалярное произведение:
AB · a = 1·2 + 1·3 + (-6)·1 = 2 + 3 - 6 = -1
|AB|² = 1² + 1² + (-6)² = 38 ⇒ |AB| = √38
|a|² = 2² + 3² + 1² = 14 ⇒ |a| = √14
cos ∠ (AB, a) = AB · a / (|AB|·|a|) = -1 / √(38·14) = -1 / √532 = -1 / (2√133)
Автор ответа:
1
Решение задания прилагаю
Приложения:
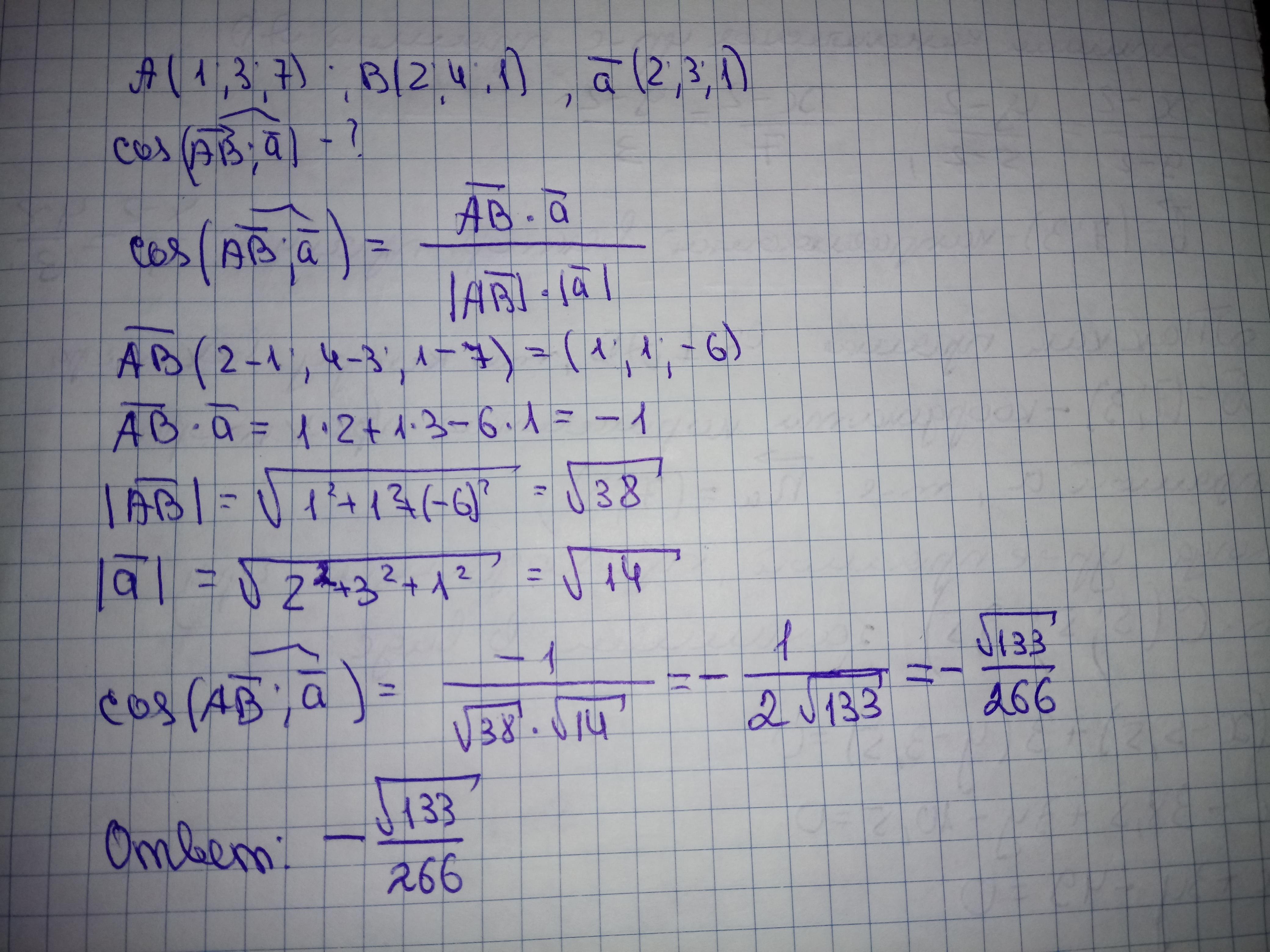
Похожие вопросы
Предмет: Математика,
автор: evabulgakova2
Предмет: Алгебра,
автор: Aigerim800
Предмет: Обществознание,
автор: kuzmenko0606
Предмет: Математика,
автор: lexa230
Предмет: Математика,
автор: gamercomputer