Question

решите задачу, 7 класс ​

Answer 1

Ответ:

по 1 признаку равенство треугольников

мы нашли сторону и два прилежащих к ней угла

Answer 2

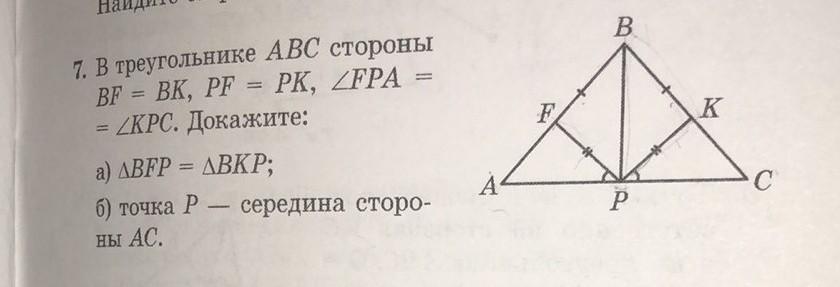
а) Рассмотрим треугольник PFB и BKP
В них: BF=BK (по условию)
FP=PK (по условию)
BP - общая
треугольники равны по трём сторонам. Из равенства треугольников следует равенство элементов => угол BFP = углу BKP, что и требовалось доказать
б) так как углы BFP и BKP равны, то смежные с ними AFP и PKC тоже будут равны.
Рассмотрим треугольники AFP и PKC
В них: FP=KP (по условию)
угол APF = углу KFC (по условию)
угол АFP = углу PKC (из ранее доказанного)
Треугольники равны по двум углом и прилежащей к ней стороне. Из равенства треугольников следует равенство элементов => АР=PC => Р - середина АС, что и требовалось доказать