Question

Решите пожалуйста Прошу Нужно очень.​

Answer 1

Ответ:

====================================

Пошаговое объяснение:

Чтобы найти промежутки монотонности, необходимо:

1. Найти производную;

2. Найти корни полученного уравнения и отметить их на числовой оси;

3. Определить знаки производной на полученных промежутках.

Если производная положительна, функция возрастает; если отрицательна - убывает.

Если производная меняет знак с "+" на "-" - точка max; с "-" на "+" - точка min.

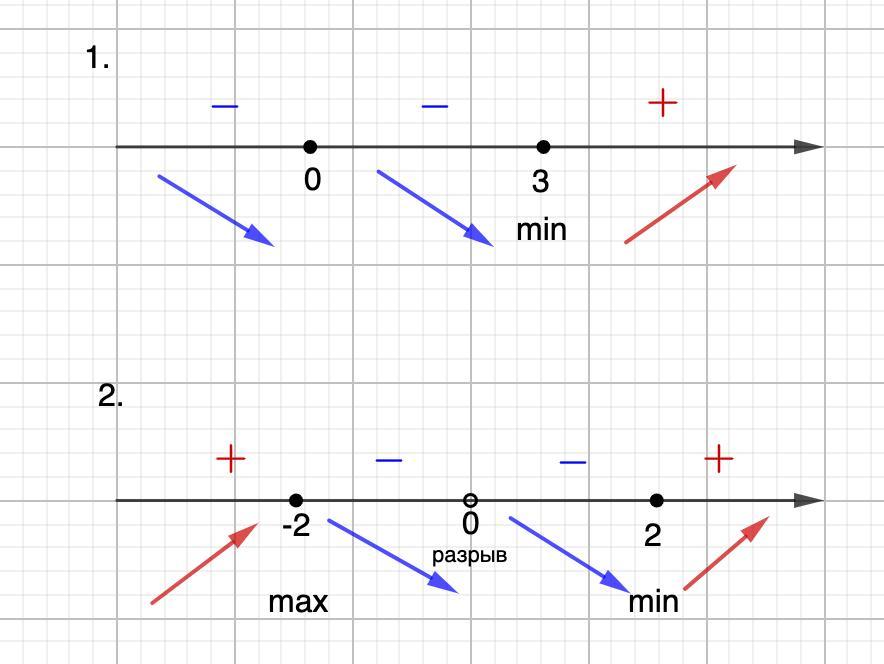
1.

$\displaystyle y=x^4-4x^3+4\\\displaystyle y'=4x^3-4*3x^2=4x^2(x-3)\\\displaystyle y'=0\;\;\;\;\;4x^2(x-3)=0\\\displaystyle x_1=0;\;\;\;x_2=3$

См. рис.

Функция убывает при х∈(-∞; 3]; возрастает при х∈[3; +∞)

Производная меняет знак с "-" на "+" в точке х=3, ⇒

$x_{min}=3$

2.

$\displaystyle y=x+\frac{4}{x}\;\;\;\;\;ODZ: x\neq 0\\\\\displaystyle y'=1+4*(-\frac{1}{x^2} ) =1-\frac{4}{x^2} =\frac{x^2-4}{x^2} \\\\y'=0\;\;\;\;\;\frac{x^2-4}{x^2} =0\;\;\;\;\;\frac{(x-2)(x+2)}{x^2}=0\\\\\displaystyle x_1=2 \;\;\;x_2=2\;\;\;x\neq 0$

См. рис.

Функция возрастает при х∈(-∞; -2]∪[2; +∞);

убывает при х∈[-2; 0)∪(0; 2]

$\displaystyle x_{max}=-2;\;\;\;x_{min}=2$

3.

$\displaystyle y=\frac{1}{8}(16-6x^2-x^3)$

1) ОДЗ: х∈R

2) Четность, нечетность:

$\displaystyle y(-x)=\frac{1}{8}(16-6*(-x)^2-(-x)^3 )=\frac{1}{8}(16-6x^2+x^3)$

$y(-x)\neq y(x)\neq -y(x)$

⇒ функция не является четной или нечетной, то есть общего вида.

3) Пересечение с осями координат:

а) с осью 0х.

$\displaystyle y=0;\;\;\;\;\;\frac{1}{8}(16-6x^2-x^3)=0 \\x_1=-5,5;\;\;\;x_2=-2;\;\;\;x_3=1,5$

(Корни найдены с помощью онлайн сервиса)

б) с осью 0у.

$x=0\;\;\;\;\;y=\frac{1}{8}(16-6*0-0)=2$

4) Функция непрерывна, критических точек нет.

Левый и правый пределы равны бесконечности ⇒ асимптот нет.

5) Возрастание, убывание, экстремумы:

Найдем производную:

$\displaystyle y'=\frac{1}{8}(0-6*2x-3x^2)=\frac{1}{8}(-12x-3x^2)\\\\\displaystyle y'=0\;\;\;\;\;\frac{1}{8}*(-3x)(4+x)=0\\\\ \displaystyle x_1=0;\;\;\;x_2=-4$

Функция возрастает при х∈[-4; 0]; убывает при х∈(-∞; -4]∪[0; +∞).

$\displaystyle x_{min}=-4;\;\;\;y_{min}=y(-4)=\frac{1}{8}(16-6*(-4)^2-(-4)^3=\frac{1}{8} (16-96+64)=-2$

$\displaystyle x_{max}=0;\;\;\;\;\;y_{max}=2$