Question

Срочно геометрия, 1,5 только. Надо записать дано доказать доказательство в доказательстве какие треугольники рассматриваем, доказываем что они равные или нет. 30 баллов

Answer 1

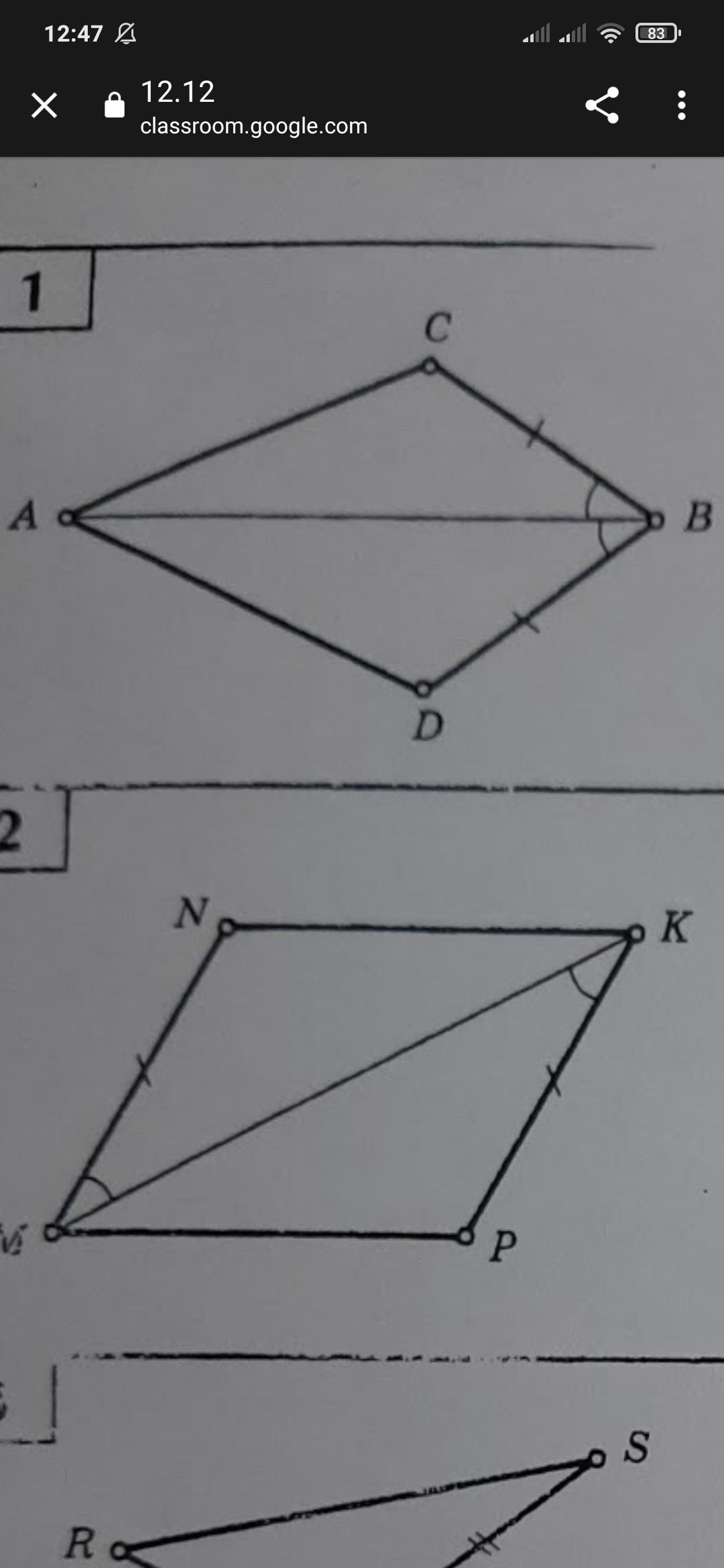
1) Дано:

<СВА = <DBA

DB = CB.

Док-ть:

∆АСВ = ∆ADB

Док-во:

Рассмотрим ∆АСВ и ∆ADB.

АВ - общая сторона.

<СВА = <DBA, DB = CB, значит ∆АСВ = ∆ADB по | признаку (по двум сторонам и углу между ними).

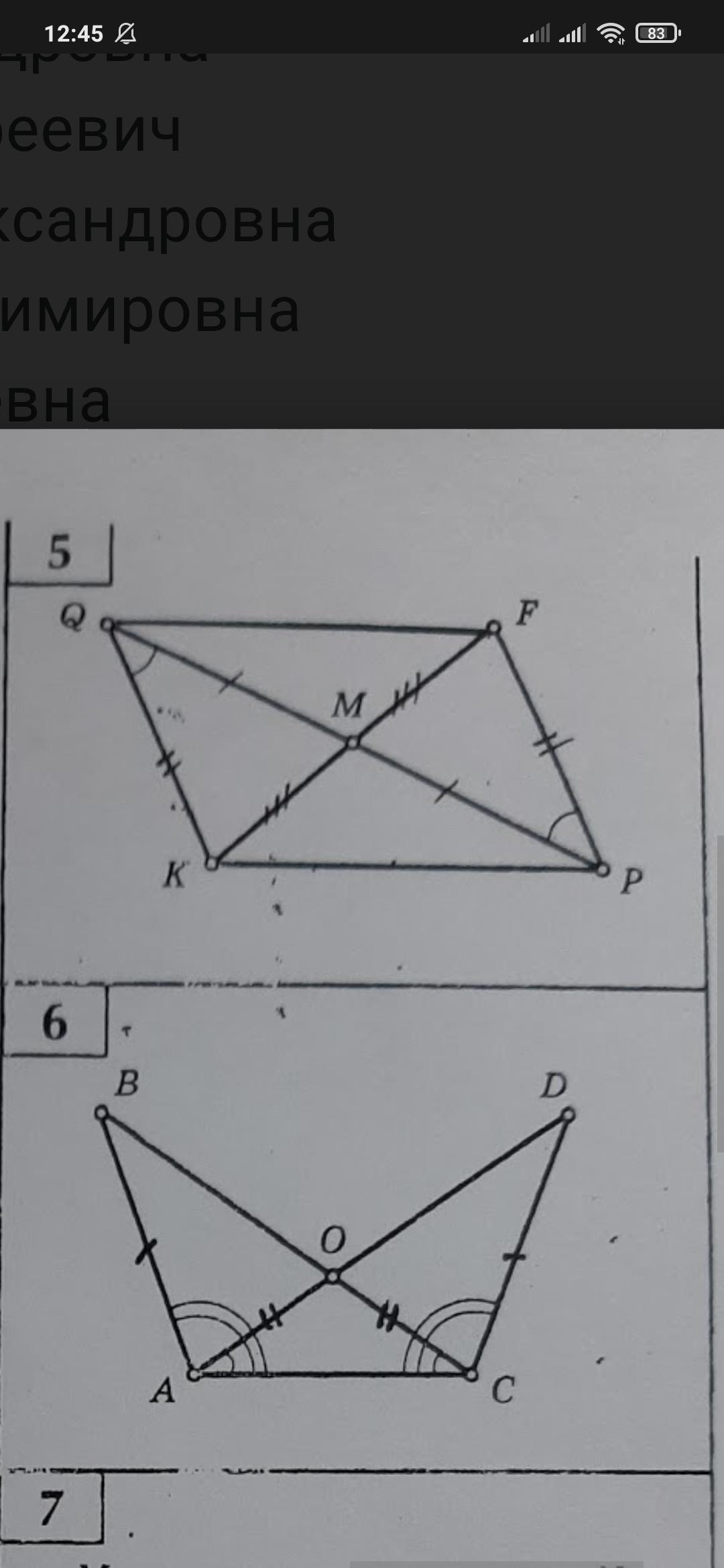
5) Дано:

QK = FP, QM = MP, KM = MF

<KQM = <FPM

Док-ть:

∆QFM = ∆KMP;

∆QKM = ∆FMP;

∆QPK = ∆QPF;

∆KQF = ∆KFP;

Док-во:

QK = FP, QM = MP, KM = MF, значит КQFP - параллелограмм.

<KQM = <FPM

1) Рассмотрим ∆QFM и ∆KMP.

<KMP = <QMP как вертикальные

QM = MP, KM = MF, значит ∆QFM = ∆KMP по | признаку.

QF = KP по св-ву параллелограмма, значит ∆QFM = ∆KMP по ||| признаку.

∆QFM = ∆KMP по | и ||| признакам.

2) Рассмотрим ∆FMP и ∆QMK.

<FMP = <QMK как вертикальные.

QK = FP, KM = MF, QM = MP, значит ∆FMP = ∆QMK по | и ||| признакам.

3) Рассмотрим ∆KQP и ∆QFP.

QK = FP, QP - общая сторона

KP = QF по св-ву параллелограмма.

<KQM = <FPM

<QKP = <QFP по св-ву параллелограмма, значит ∆KQP = ∆QFP по | , || , ||| признакам.

4) Рассмотрим ∆KQF и ∆KFP.

KF - общая сторона.

QK = FP, QF = KP.

<KQF = <FPK.

∆KQF и ∆KFP по | , || , ||| признакам.

ч.т.д