Предмет: Математика,
автор: dinehip478
Решение неопределённого интеграла
Приложения:
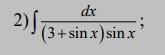
Ответы
Автор ответа:
0
Ответ:
Сделаем тригонометрическую замену:
Разложим дробь на простейшие:
система:
Получаем интегралы:
выделим в знаменателе квадрат:
собираем все вместе:
переходим от замены:
- итоговый ответ.
Miroslava227:
надеюсь, нигде не ошиблась
Похожие вопросы
Предмет: Русский язык,
автор: Nikkanor
Предмет: Математика,
автор: КаТюШшА039
Предмет: Русский язык,
автор: Алина06222006
Предмет: Обществознание,
автор: Lizo4kaLL
Предмет: Информатика,
автор: just2nd