Предмет: Математика,
автор: LSM54
Очень нужно, пожалуйста, решите! 30 баллов!!
Найдите пределы
Приложения:
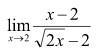

Ответы
Автор ответа:
0
Ответ:
1) 2; 2) -4.
Пошаговое объяснение:
№1
=
Домножим числитель и знаменатель на , получим:
+1=2
№2
=
Домножим числитель и знаменатель на +2, получим:
(-
-2)=-4
LSM54:
Помогите, пожалуйста, с еще одним заданием https://znanija.com/task/41047832
То задание сильно подольше, попозже может сделаю.
Похожие вопросы
Предмет: Английский язык,
автор: kaban117
Предмет: Алгебра,
автор: dzhanaiedvina
Предмет: Русский язык,
автор: vikkab74Vikila
Предмет: Алгебра,
автор: lisa17032
Предмет: История,
автор: Аноним