Предмет: Математика,
автор: mariyabliznuk61
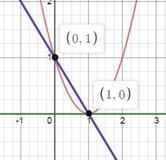
Сделайте чертёж и вычислите площадь фигуры, ограниченной данными линиями:
y=(x-1)^2; y=1-x; y=0
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
из чертежа виден интеграл
пределы по х от 0 до 1
у₁=1-х
у₂=(х-1)²
считаем первый потом второй
производим замену u = 1-x, du = dx, и пересчитаем пределы интегрирования нижний u = -1, верхний u = 0
итого 1/2 -1/3 = 1/6
Приложения:
Похожие вопросы
Предмет: Математика,
автор: matanya43x
Предмет: Математика,
автор: kyrych
Предмет: Русский язык,
автор: zhekabacheriko
Предмет: Математика,
автор: софия733
Предмет: Литература,
автор: artemcvert