Предмет: Математика,
автор: 777anvarrr777
Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций (ось вращения – ось
Ox ): y=5cosx , y=cosx , x=0 , x≥0
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
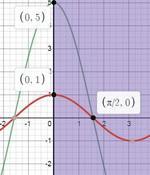
рисуем графики и видим пределы интегрирования по х (0;π/2)
и наш объем рассчитываем ка разность объемов тел, образованныx вращением кривых y₁=5cosx , y₂=cosx
по формуле
сначала посчитаем интеграл
после замены пересчитаем пределы интегрирования: верхний u = π; нижний u = 0
и теперь объем
Приложения:
Похожие вопросы
Предмет: Математика,
автор: senaj
Предмет: Математика,
автор: supersp1977
Предмет: Русский язык,
автор: дина32100
Предмет: Математика,
автор: kristishkalniza
Предмет: История,
автор: MariselMaz