Предмет: Математика,
автор: 777anvarrr777
Продифференцировать данные функции, используя правило логарифмического дифференцирования:
Приложения:
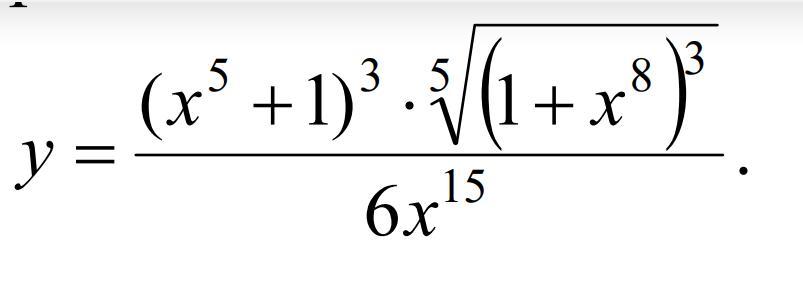
Ответы
Автор ответа:
2
Ответ:
Формула:
Похожие вопросы
Предмет: Русский язык,
автор: 19864
Предмет: Русский язык,
автор: norik31072014
Предмет: Биология,
автор: chernovolova
Предмет: Геометрия,
автор: павлуха3
Предмет: Геометрия,
автор: dgnhh4444
https://znanija.com/task/41045693