Предмет: Математика,
автор: calmanov12
ребят один пример,ради света
Приложения:
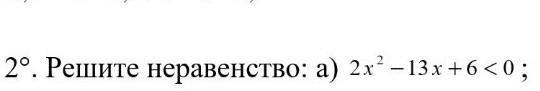
Ответы
Автор ответа:
0
Ответ:
x1=-6,x2=-0,5.
Пошаговое объяснение:
2x^2-13x+6<0
Решим через дискриминант.
Формула Д=b^2-4ac.
D=13^2-4×2×6=169-48=121.
Дальше по формуле ищем иксы.
x1=-b-корень из дискриминанта/2а
x2=-b+ корень из дискриминанта/2а
x1=-13- корень из 121/2×2
x2=-13+ корень из 121/2*2
x1=-24/4=-6
x2=-2/4=-0,5
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Найдём нули функции:
Определим знаки неравенства на интервалах
Неравенство принимает отрицательное значение на интервале
значит,
Похожие вопросы
Предмет: Математика,
автор: qqccssyy123
Предмет: География,
автор: alesh9901544
Предмет: Математика,
автор: cepnat2013
Предмет: Алгебра,
автор: senin041
Предмет: Физика,
автор: Decon1337