Предмет: Математика,
автор: NikitosFoxPlay
Нужна полное решения
Приложения:
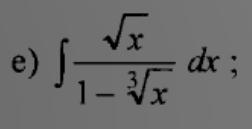
Ответы
Автор ответа:
1
Ответ:
Замена:
Разделим числитель на знаменатель:
Похожие вопросы
Предмет: География,
автор: дрищь
Предмет: Математика,
автор: 2klass1
Предмет: Английский язык,
автор: olgaei28
Предмет: Физика,
автор: Motyymniy
Предмет: Психология,
автор: марха38