Предмет: Алгебра,
автор: skzstay
помогите решить систему уравнений пожалуйста
Приложения:
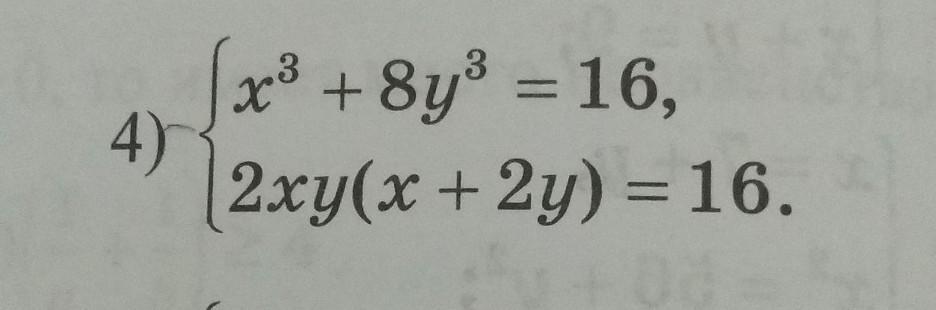
Ответы
Автор ответа:
0
Ответ:
Объяснение:
ОДЗ:
Решение:
Похожие вопросы
Предмет: Биология,
автор: 878р
Предмет: История,
автор: DiМан2
Предмет: Химия,
автор: Olya545
Предмет: Математика,
автор: TimPro1
Предмет: Литература,
автор: света1146