Предмет: Геометрия,
автор: aleshkalolev
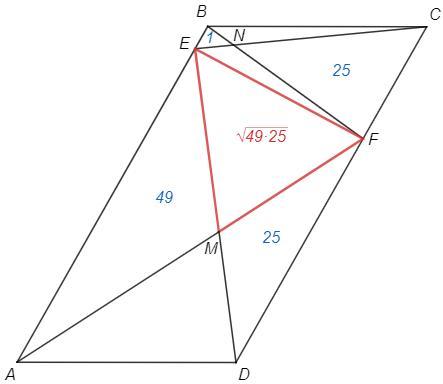
На сторонах AB и CD параллелограмма ABCD отмечены точки E и F соответственно. Отрезки AF и DE пересекаются в точке M, а отрезки BF и CE в точке N.
S AME=49
S ENB=1
S CNF=25.
Найдите S MEF
Ответы
Автор ответа:
0
S(ABF) =S(CDE) (равные основания, общая высота)
Вычитая общую часть ENFM, получаем
S(AME)+S(ENB) =S(CNF)+S(FMD) => S(FMD) =49+1-25 =25
S(AEF)=S(AED) (общие основание и высота)
S(MEF) =S(AEF)-S(AME) =S(AED)-S(AME) =S(AMD)
S(AME)/S(MEF) =AM/MF =S(AMD)/S(FMD) (общая высота => площади относятся как основания)
S(MEF)*S(AMD) =S(AME)*S(FMD) =>
S(MEF) =√(S(AME)*S(FMD)) =√(49*25) =35
Приложения:
siestarjoki:
Диагонали делят трапецию на четыре треугольника. Если площади треугольников при основаниях S1 и S2, то площади треугольников при боковых сторонах √(S1*S2), а площадь трапеции (√S1+√S2)^2
Похожие вопросы
Предмет: Математика,
автор: YasminaJust
Предмет: Алгебра,
автор: ЛёЛик19991
Предмет: Химия,
автор: sinmax99
Предмет: Математика,
автор: Аооарао
Предмет: Математика,
автор: SuperEpicGirl