Question

100 БАЛЛОВ !!! Брусок движется по наклонной плоскости под углом α=60° к горизонту без начальной скорости. Выберите правильную формулу, описывающую изменение импульса тела в процессе прохождение через точки 1 и 2 (см. рисунок) в проекции на ось X, направленную по движению тела.




m(v1−v2)=Δt⋅mg⋅(3√2−μ12)

m(v2−v1)=Δt⋅mg⋅(3√2−μ12)

m(v1−v2)=Δt⋅mg⋅(12−μ3√2)

m(v2−v1)=Δt⋅mg⋅(12−μ3√2)

m(v2−v1)=Δt⋅mg⋅(3√2−μ3√2)

Answer 1

Дано:

α = 60°

μ

m(v₂ - v₁) - ?

Очевидно, что при спуске вниз тело будет иметь больше скорости, если оно прошло большее расстояние. Поэтому стоит отнимать от большего импульса меньший, то есть, формулы (1) и (3) отпадают.

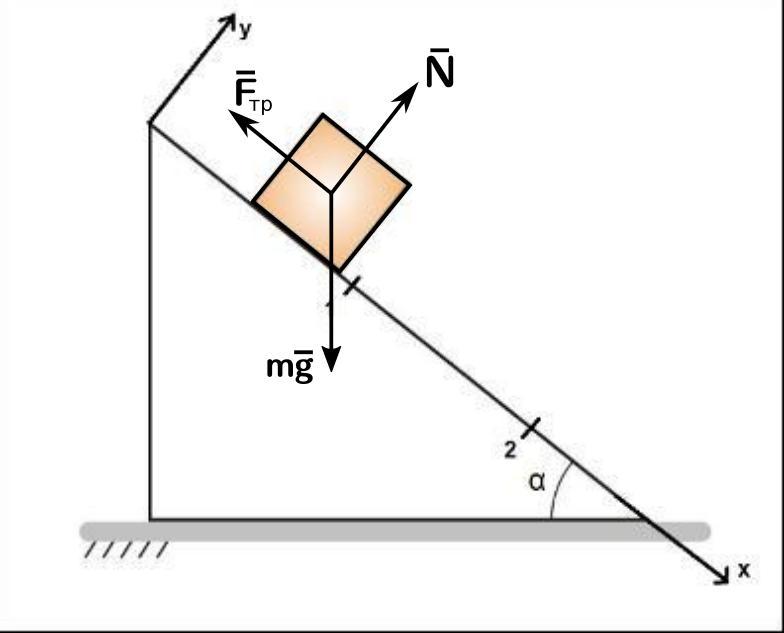
Изобразим силы на рисунке и запишем второй закон Ньютона в векторной форме, и спроецируем его:

$m\vec{a} = m\vec{g} + \vec{N} + \vec{F}_{tr}\\OX: mgsin\alpha - F_{tr} = ma\\OY: mgcos\alpha = N\\ma = mg\sin{\alpha}-N \mu = mg(\sin{\alpha} - \mu \cos{\alpha})\\a = g(\sin{\alpha}- \mu \cos{\alpha})$

Мы получили ускорение тела по оси Ох.

Из кинематических формул скорости при равноускоренном движении:

$v_2 = v_1+at\\mv_2 - mv_1 = m(v_2-v_1) = mat = tmg(\sin{\alpha} - \mu \cos{\alpha})\\m(v_2-v_1) = \Delta{t} * mg* (\dfrac{\sqrt{3}}{2} - \mu \dfrac{1}{2})$

Ответ: вторая формула.