Предмет: Геометрия,
автор: dsr20061106
Даю 70 баллов...не люблю тех кто не правильно отвечает.....с решением....
Приложения:
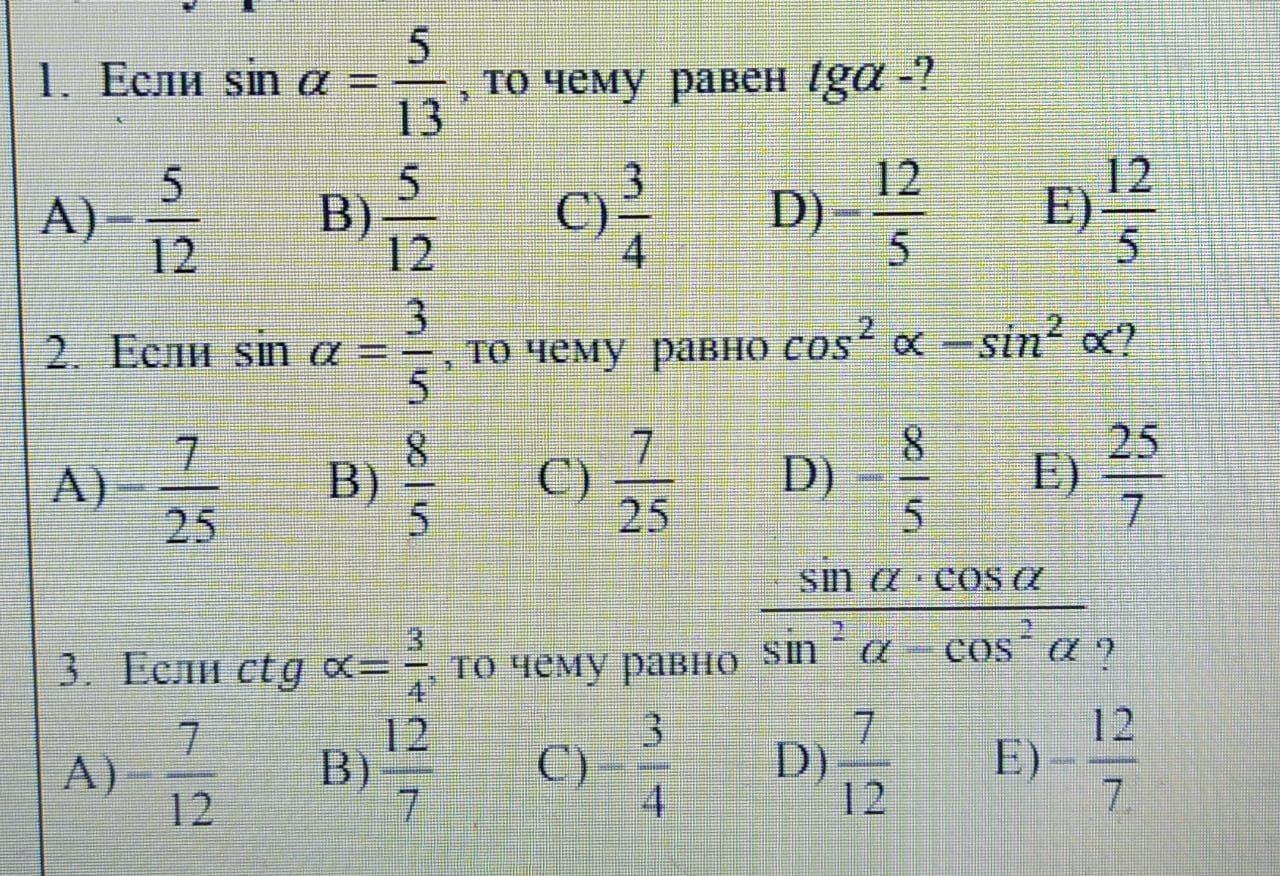
Ответы
Автор ответа:
1
Ответ:
Я решала тебе уже такие задания с подробным объяснением, так что здесь так же по тем же формулам выражаем и подставляем - и готово!
1.
Теперь можно найти тангенс:
Правильный ответ под буквой B
2. Сначала найдём косинус, а потом просто подставим в необходимое выражение.
Правильный ответ под буквой C
RybaVoblla:
Прости, я не решила третье задание
спасибо все равно
Похожие вопросы
Предмет: Литература,
автор: Виктория10
Предмет: Другие предметы,
автор: UZHITEL
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: DamyanWhite
Предмет: Химия,
автор: Merzz