Предмет: Математика,
автор: palkovnikgineral
Помогите решить 25Б..
Приложения:
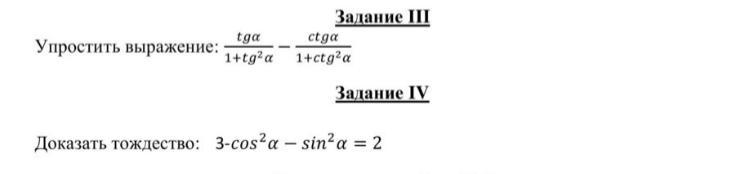
Ответы
Автор ответа:
0
Ответ:
3.
Воспользуемся формулам:
4.
Похожие вопросы
Предмет: Математика,
автор: dmitrievnasofi
Предмет: Математика,
автор: кристина108
Предмет: Математика,
автор: savchukvalya20
Предмет: Математика,
автор: nastyakramskay
Предмет: ОБЖ,
автор: Алинкамалинка2107