Предмет: Геометрия,
автор: vityagolovko2004
Из вершины среднего угла треугольника к его плоскости проведён перпендикуляр,равный 3 см.Определить расстояние от концов перпендикуляра до противолежащей стороны треугольника,стороны каждого равны 9 см,10 см и 11 см. Помогите, пожалуйста. Очень надо, пожалуйста
Ответы
Автор ответа:
2
Ответ:
6√2 см
9 см
Объяснение:
Средний по величине угол лежит против средней по величине стороны треугольника.
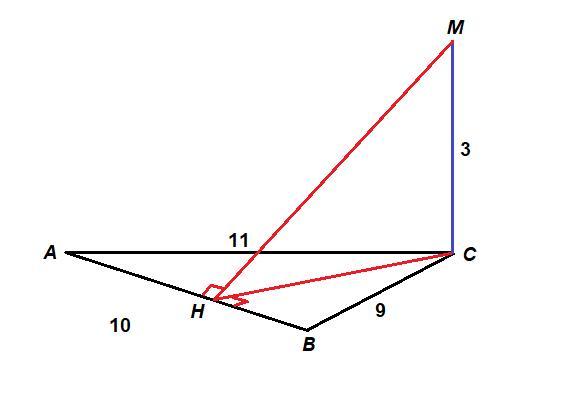
АВ = 10 см - средняя сторона, значит перпендикуляр к плоскости треугольника АВС проведен из вершины С - МС.
Проведем СН⊥АВ - высоту ΔАВС.
СН - проекция наклонной МН на плоскость (АВС), значит
МН⊥АВ по теореме о трех перпендикулярах.
СН и МН - искомые расстояния.
Найдем площадь ΔАВС по формуле Герона:
где р - полупериметр.
см²
Найдем высоту СН:
см
ΔМСН: ∠МСН = 90°, по теореме Пифагора
см
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: Nikolaevakunne
Предмет: Математика,
автор: shestova12345
Предмет: Геометрия,
автор: ученик1894
Предмет: Математика,
автор: максмаксзк