Предмет: Алгебра,
автор: sabi0000
Срочно! Помогите пожалуйста!
Надо срочно сдать
Приложения:
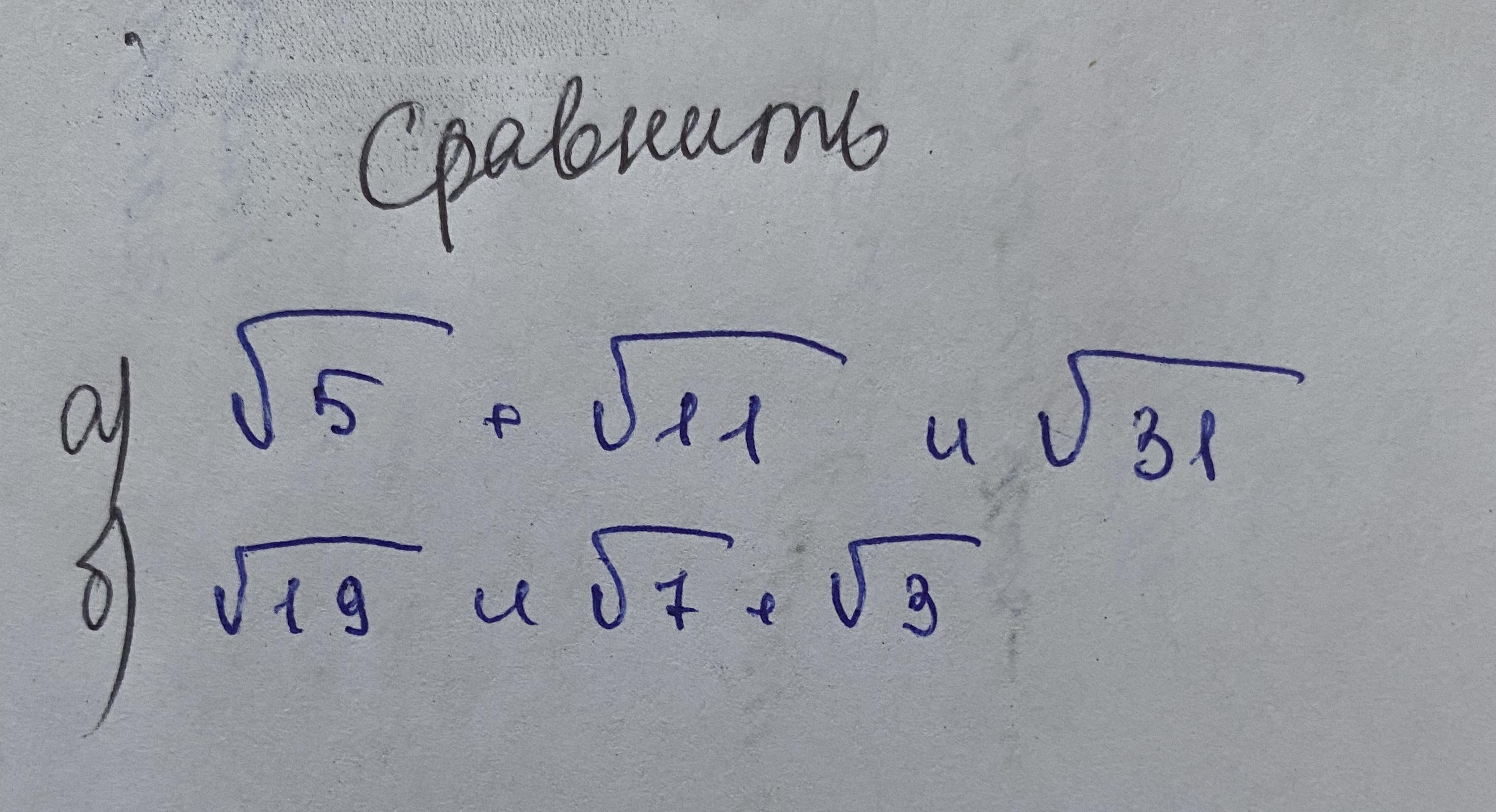
Ответы
Автор ответа:
0
Ответ:
Решение:
Сравнить:
а).
Все члены положительные,
обе части неравенства возво
дим в квадрат:
Обе части неравенства возво
дим в квадрат:
==>
b.
Сравнить:
Обе части возводим в квадрат:
Возводим в квадрат левую и
правую части неравенства:
==>
Похожие вопросы
Предмет: Русский язык,
автор: Alin4kag17
Предмет: Русский язык,
автор: Iryzik1
Предмет: Математика,
автор: tanyyuscha
Предмет: Биология,
автор: vasylina2606