Предмет: Математика,
автор: den2702
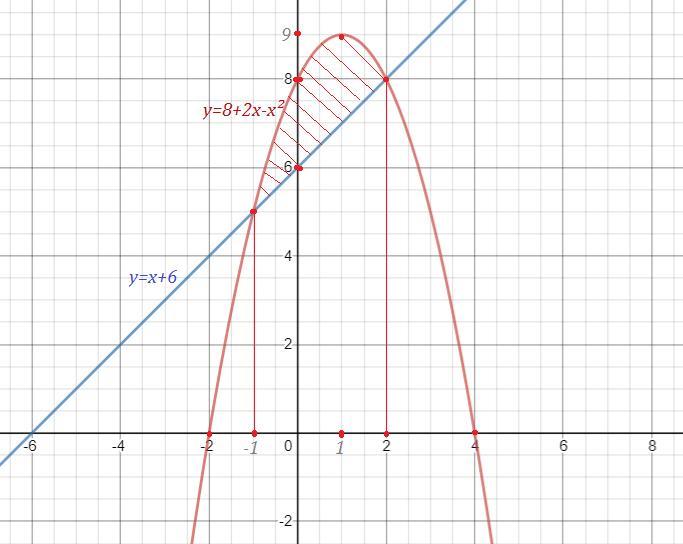
Применение определенных интегралов для вычисления найти объем тел вращения.
y=8+2x-x^2
y=x+6
Пример на картинке
Приложения:

Ответы
Автор ответа:
2
Приложения:
den2702:
спасибо
написала площадь, сейчас напишу объём ...
Автор ответа:
2
Пошаговое объяснение:
Ответ: V≈209,23 куб. ед.
Похожие вопросы
Предмет: Математика,
автор: musa2004
Предмет: Русский язык,
автор: matveevakete
Предмет: Математика,
автор: vlad964
Предмет: Математика,
автор: kamillamagomed
Предмет: Алгебра,
автор: Khatagov1