Question

Геометрия 8 класс Площадь четырехугольника

Answer 1

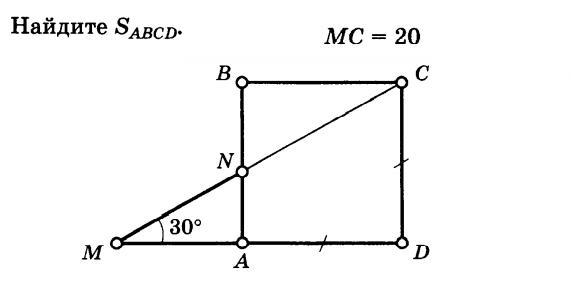
Рассмотрим $\bigtriangleup$MCD:

$\angle MDC = 90^o$

MC = 20 (гипотенуза в прямоугольном треугольнике)

$\angle M = 30^o$

Катет, лежащий напротив угла с градусной мерой 30°, равен половине гипотенузы, тогда $CD = \frac{MC}{2} = \frac{20}{2} = 10$.

Рассмотрим $\Box$ABCD:

$\angle ADC = 90^o$, значит ABCD - прямоугольник.

$AD = DC$. Если в прямоугольнике две смежные стороны равны, то он является квадратом, значит, ABCD - квадрат.

$S_{ABCD} = CD^2 = 10^2 = 100$.

Ответ: 100.

Answer 2

Ответ:

Объяснение:

Так как треугольник MCD является прямоугольным, а угол М равен 30° то тогда выходит что катет CD=MC/2 CD=20/2=10. Так как AD=CD а угол D=90° то S(abcd)=10*10=100