Предмет: Алгебра,
автор: aleksoref
Здравствуйте, помогите пожалуйста
24,6 и 24,8
Приложения:
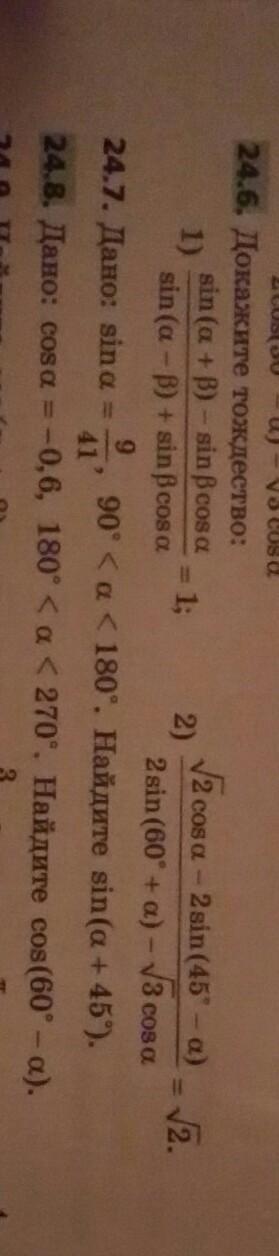
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: 26021999
Предмет: Математика,
автор: makskovalev1995
Предмет: Химия,
автор: Саяе32
Предмет: Биология,
автор: Tim545352
Предмет: Алгебра,
автор: 2004илья