Предмет: Математика,
автор: Аноним
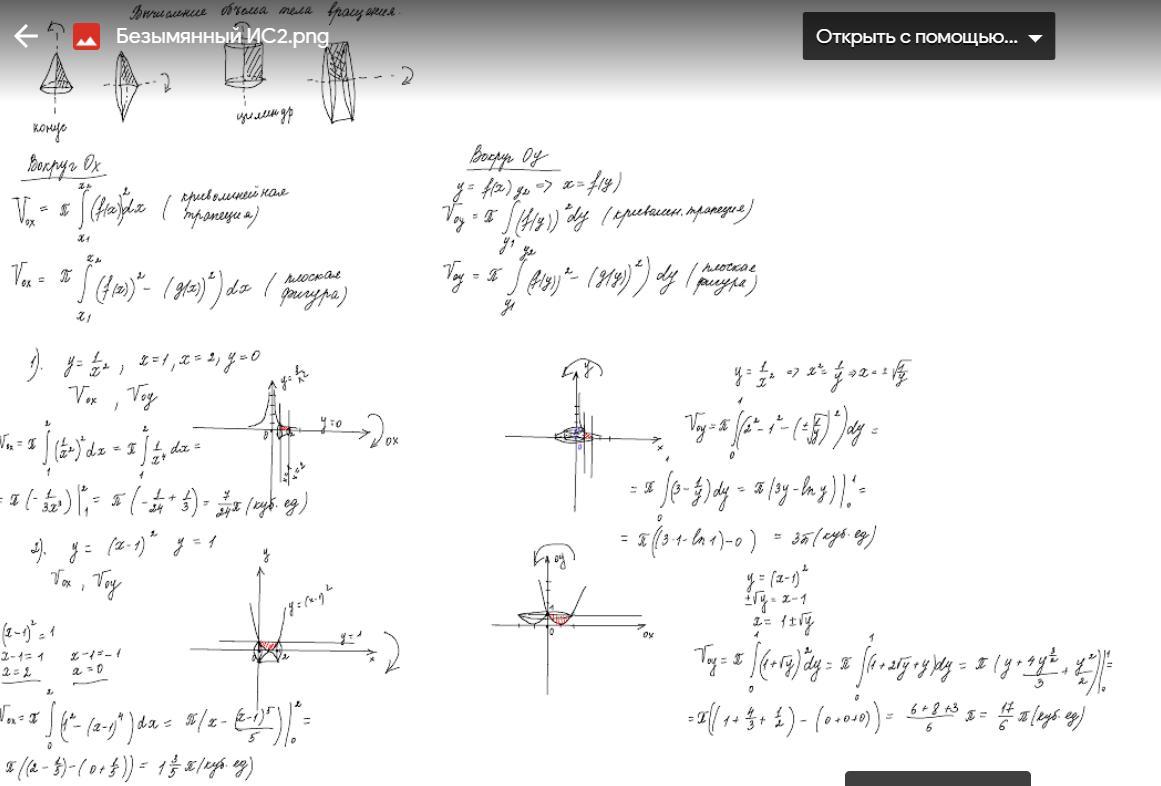
Применение определенных интегралов для вычисления
найти объем тел вращения. xy=6 x+y-7=0
Внизу пример
Приложения:
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
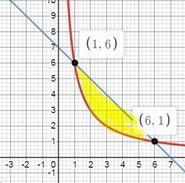
я так понимаю, что вращаем вокруг оси ОХ
запишем уравнения в виде
у₁ = 7- х; у₂= 6/х
находим точки пересечения: 7-х = 6/х ⇒ х₁ = 1; х₂ = 6
рисуем графики
в таких случаях требуемый объем ищут как разность объемов
сначала посчитаем интеграл
сделаем замену u = (7-x), du = (-dx), и пересчитаем пределы интегрирования верхний предел u=7-6=1, нижний предел u=7-1=6
умножим на -1, чтобы привести пределы в правильную последовательность
теперь
и вот
Приложения:
Аноним:
вы моежете зайти в дискорд ?
увы. у меня такого нет
Похожие вопросы
Предмет: Математика,
автор: faflyu
Предмет: Алгебра,
автор: berenzon
Предмет: Русский язык,
автор: TheMCMrSkinerDJ
Предмет: История,
автор: kruglikov01
Предмет: Математика,
автор: ralinagumarova2