Предмет: Геометрия,
автор: nikita98464
на рисунке 96 AC=AD,AB CD.докажите ,что BC=BDи<ACB=<ADB
Приложения:
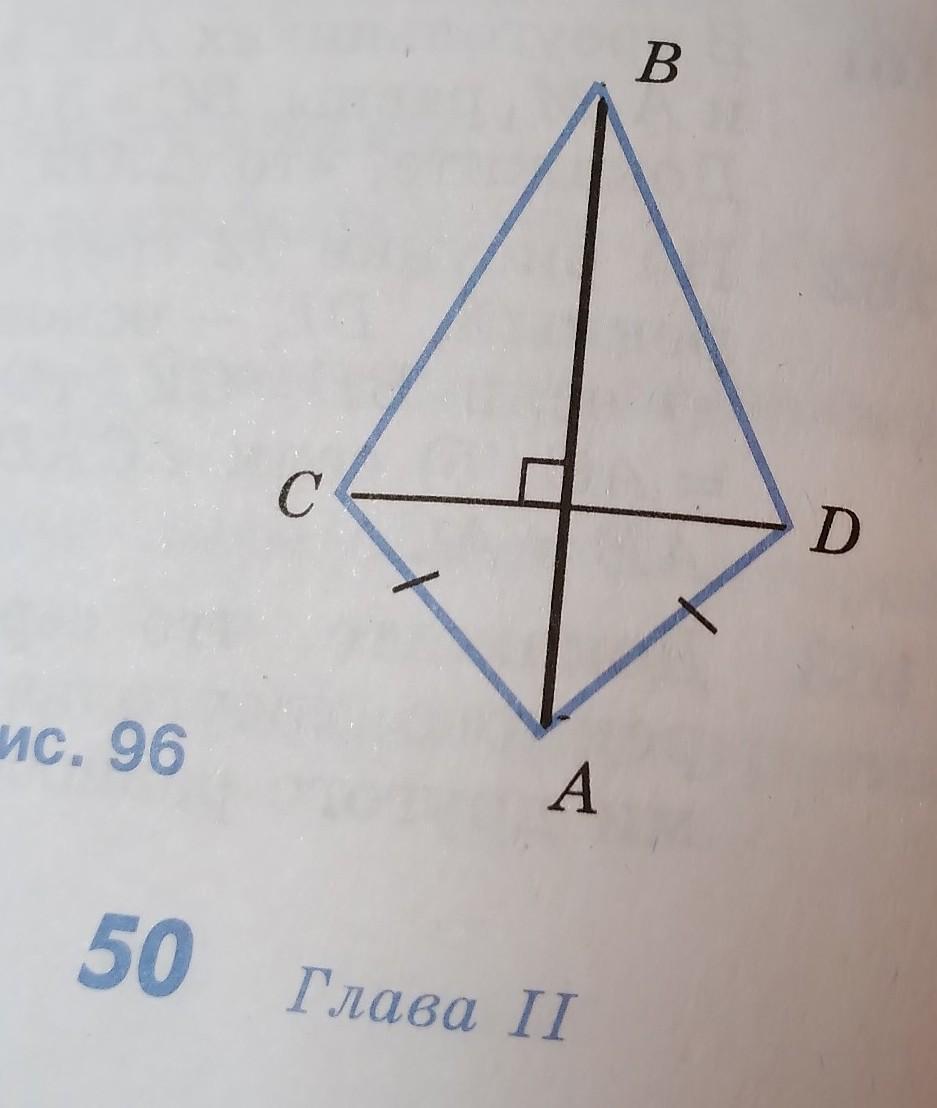
Ответы
Автор ответа:
5
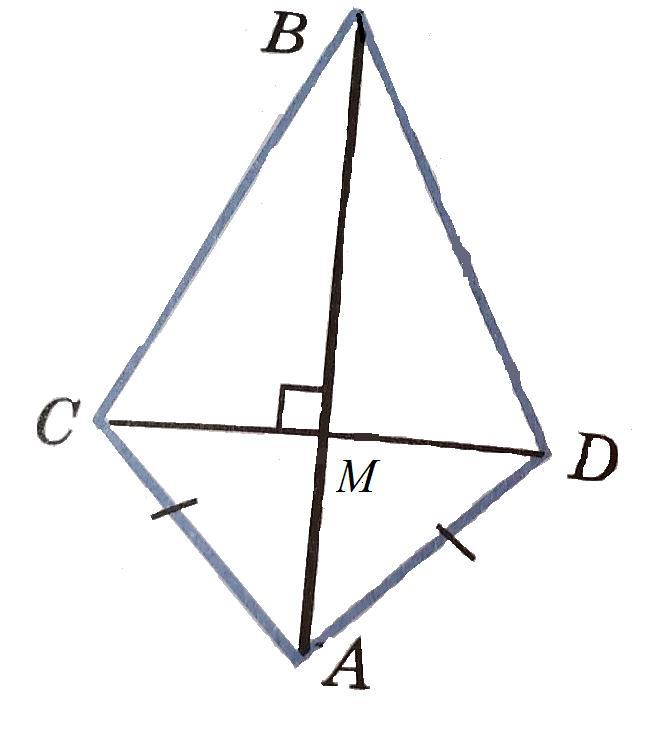
См. рисунок.
Т.к. АС = АD, то ΔАСD - равнобедренный.
Т.к. АВ ⊥ СD и АВ ∩ СD = М, то АМ - высота равнобедренного ΔАСD, а, значит, АМ - медиана, т.е. М - середина СD.
Рассмотрим ΔСВD. Т.к. ВМ - высота и медиана, то ΔВСD - равнобедренный (по признаку равнобедренного треугольника), следовательно, ВС = ВD.
Имеем: АС = АD (по условию), ВС = ВD (по доказанному), АВ - общая сторона, тогда ΔАВС = ΔАВD по трем сторонам.
Из равенства треугольников следует, что ∠АСВ = ∠АDВ.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: natalimingaleeva
Предмет: Русский язык,
автор: mari901
Предмет: Математика,
автор: vkoplak
Предмет: Математика,
автор: vladturgenbaev
Предмет: Математика,
автор: shalimova382