Question

В выпуклом четырехугольнике abcd сторона bc вдвое меньше, чем ad. диагональ ac перпендикулярна стороне cd а диагональ bd перпендикулярна стороне ab. найдите меньший острый угол этого четырехугольника, если больший равен 67. ​

Answer 1

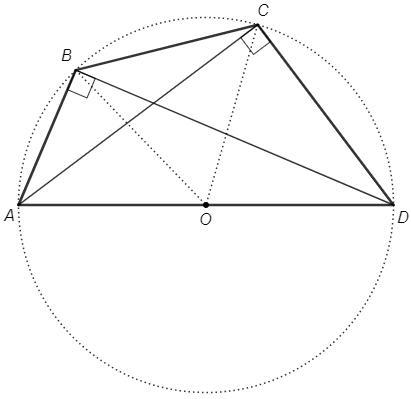
По условию углы ABD и ACD - прямые.

Отрезок AD виден из точек B и С под прямым углом, следовательно точки B и С лежат на окружности диаметром AD.

Очевидно, что углы B и С больше прямого (тупые).

Пусть ∠A=67

∠ADB=90-67=23

O - середина AD

AD/2 =OB=OC (радиусы) =BC => △BOC - равносторонний, ∠BOC=60

∠BDC =∠BOC/2 =30 (вписанный угол равен половине центрального, опирающегося на ту же дугу)

∠D =∠ADB +∠BDC =23+30 =53°