Question

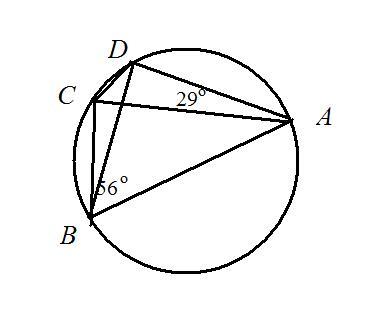
четырехугольник ABCD вписан в окружность. Угол ABC равен 56, угол CAD равен 29. Найдите угол ABD. Ответ дайте в градусах

Answer 1

Т.к. четырехугольник ABCD вписан в окружность, то по свойству вписанного четырехугольника сумма противоположных углов равна 180°, т.е. ∠АВС + ∠АDС = 180°, откуда ∠АDС = 180° - ∠АВС = 180° - 56° =

= 124°.

В ΔСDА известно, что ∠САD = 29°, ∠АDС = 124°, значит,

∠DСА = 180° - (∠САD + ∠ АDС) = 180° - (29° + 124°) = 180° - 153° = 27°.

По свойству вписанного угла этот угол равен половине дуги, на которую он опирается.

Т.к. ∠САD, ∠DСА и ∠АВD - вписанные, то дуга DА = 2∠DСА = 2 · 27° =

= 54°.

∠АВD также вписанный и опирается на дугу DА, значит,

∠АВD равен половине дуги DА, т.е. ∠АВD = 27°.

Ответ: 27°.