Question

очень срочно!!!
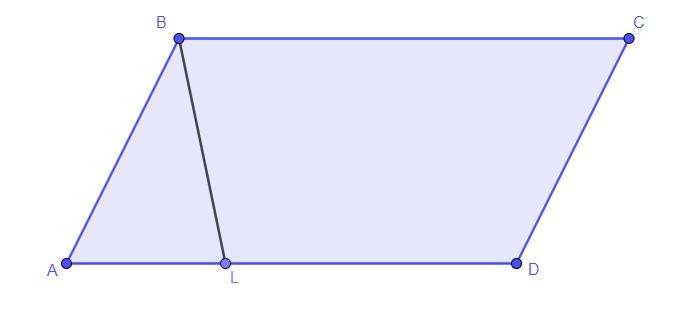
Дан параллелограмм ABCD, ∠D=100∘, BC=39 . На стороне AD есть такая точка L, что ∠ABL=50∘, LD=13. Найдите длину CD.

Answer 1

Ответ:

26

Объяснение:

сначала нужно найти AL: AL=BC-LD=39-13

затем находим угол А

для этого нужно найти угол С

он будет равен 80,потому что сумма углов в четырехугольнике равна 360 градусам (100+50+130+х=360;х=80)

находим угол BLA: 180-50-80=50

угол В=углу BLA => треугольник ABL равнобедренный

значит AB=AL=26

Answer 2

Ответ:

CD = 26 см

Объяснение:

Дано: ABCD - параллелограмм, ∠ADC = 100°, ∠ABL = 50°, BC = 39, LD = 13

Найти: CD - ?

Решение: Так как по условию ABCD - параллелограмм, то его противоположные стороны и углы равны по свойствам параллелограмма следовательно, AB = CD, AD = BC, ∠ADC = ∠ABC,

∠BAD = ∠BCD. Так как BC = AD, то BC = AL + LD ⇒ AL = BC - LD = 39 - 13 =  = 26 см. По определению параллелограмма, его противоположные стороны параллельны, следовательно $AB \parallel CD$, тогда ∠BAD и ∠ADC - внутренние разносторонние углы при секущей, по свойству внутренних разносторонних углов их сумма 180°, тогда ∠BAD + ∠ADC = 180° ⇒ ∠BAD = 180° - ∠ADC = 180° - 100° = 80°. Рассмотрим треугольник ΔBAL. По теореме про сумму углов треугольника:

∠BAL + ∠ALB + ∠ABL =  180° ⇒ ∠ALB = 180° - ∠BAL - ∠ABL = 180° - 80° - 50° = 50°.  По теореме так как ∠ALB = ∠ABL = 50°, то треугольник ΔBAL - равнобедренный с основанием BL, тогда AB = AL = 26 см. Так как

AB = CD, то CD = 26 см.