Question

Большая из сторон параллелограмма равна 14 см, а его высоты равны 5см и 7 см. Найдите меньшую сторону параллелограмма.
Найдите площадь параллелограмма, если две стороны его равны 23 см и 11 см, а угол между ними равен 30.

Answer 1

Ответ:

1. 10 см; 2. 126,5 см²

Объяснение:

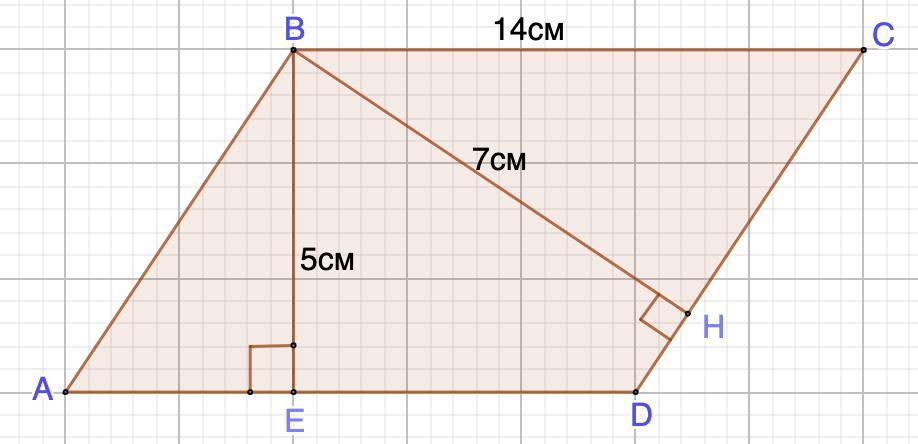
1. Дано: ABCD - параллелограмм;

AD = ВС = 14 см; ВЕ = 5 см; ВН = 7 см.

Найти: DC

Решение:

Площадь параллелограмма равна произведению основания на высоту.

⇒ S = AD*BE = DC*BH

14*5 = DC*7

$\displaystyle DC=\frac{14*5}{7}=10\;_{(CM)}$

2. Дано: параллелограмм;

Стороны равны a=23 см и b=11 см.

Угол между ними α=30°.

Найти: S

Решение:

Площадь параллелограмма равно произведению смежных сторон на синус угла между ними.

S = ab*sinα

S = 23*11*sin30° = 23*11*0,5 = 126,5 (см²)