Question

В прямоугольном треугольнике ABC, ∠C = 90° и точка K лежит на катете BC. Эта точка находится на равном расстоянии от AB и AC. Если KC = 2,7 и AK = 4,1 то найди острые углы треугольника ABC.
Округли ответ до десятых.
∠A =
∠B =
ПОЖАЛУЙСТА Очень ПРОШУ

Answer 1

Ответ:

∠A = 82,4°

∠B = 7,6°

Объяснение:

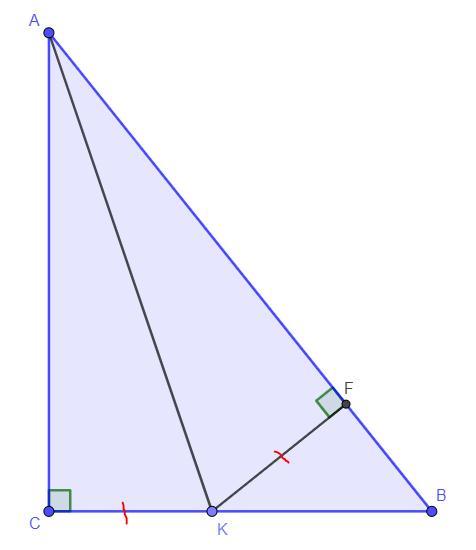
Дано: ∠C = 90°, K ∈ BC, CK = KF, CK ⊥ AC, KF ⊥ AB, KC = 2,7; AK = 4,1

Найти: ∠A, ∠B - ?

Решение: Так как по условию CK = KF, то KF = 2,7 .Рассмотри треугольник ΔAKF. Так как по условию KF ⊥ AB, то треугольник ΔAKF - прямоугольный. $\sin \angle KAF = \dfrac{KF}{AK} = \dfrac{2,7}{4,1} \approx 0,6585$. Рассмотри треугольник ΔACK. Так как по условию ∠C = 90°, то треугольник ΔACK - прямоугольный, тогда $\sin \angle CAK = \dfrac{CK}{AK} = \dfrac{2,7}{4,1}\approx 0,6585$.

∠KAF = arcsin(sin ∠KAF) = arcsin(0,6585) ≈ 41.2°.

∠CAK = arcsin(sin ∠CAK) = arcsin(0,6585) ≈ 41.2°.

∠CAB = ∠KAF + ∠CAK = 41.2° + 41.2° ≈ 82,4°.

По теореме про сумму углов треугольника: ∠C + ∠CAB + ∠CBA = 180°⇒

⇒ ∠CBA = 180° - ∠C - ∠CAB = 180° - 90° - 82,4° = 7,6°.

∠A = ∠CAB ≈ 82,4°.

∠B = ∠CBA ≈ 7,6°.