Предмет: Алгебра,
автор: avakinlove
Вычислить Sin (α+ β), Cos (α – β), Cos 2β, Sin 2α, tg2α, если...
Приложения:
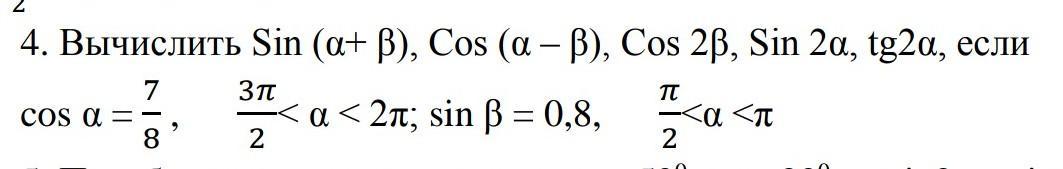
Ответы
Автор ответа:
4
Ответ:
угол а принадлежит 4 четверти => sina отрицательный
угол в принадлежит 2 четверти => cosв отрицательный.
Нашли необходимое, перейдём к вопросам задания.
djfjfjrjdjj:
здравствуйте, вы бы не могли бы мне помочь?
заранее спасибо
Похожие вопросы
Предмет: Математика,
автор: Likasa
Предмет: История,
автор: krutoy12345
Предмет: Математика,
автор: Sashaspilka
Предмет: Математика,
автор: Jakai2808
Предмет: Биология,
автор: saenara05