Предмет: Математика,
автор: daiyrbekbibota
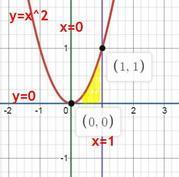
Найдите объем фигуры, полученной вращением криволинейной трапеции, ограниченной линиями y=x2, x=0 и x=1, y=0 вокруг оси абсцисс
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
y=x², x₁=0 и x₂=1, y=0 вокруг оси абсцисс
сначала рисуем графики и сразу видим, что у нас получается "воронка"
у₁ = х²; у₂ = 0
итак, считаем определенный интеграл
Приложения:
Автор ответа:
0
Ответ:
кубических единиц
Пошаговое объяснение:
Надо посчитать тройной интеграл. (чтобы не помнить никаких других формул)
пределы интегрирования:
y изменяется от 0 до ;
x изменяется от 0 до 1;
угол поворота α меняется от 0 до 2π (полный поворот)
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: 3цц
Предмет: Математика,
автор: bk34
Предмет: Математика,
автор: Chokkolina