Предмет: Алгебра,
автор: dixiefixie
решите второе, пожалуйста❤️
Приложения:
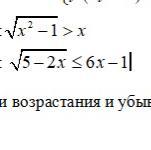
Ответы
Автор ответа:
1
Объяснение:
ОДЗ:
2x-1=0 x=0,5
9x+2=0 x=-2/9.
-∞__+__-2/9__-__0,5__+__+∞
x∈(-∞;-2/9]U[0,5;+∞)
Согласно ОДЗ:
Ответ: x∈[0,5;2,5].
Похожие вопросы
Предмет: Химия,
автор: oosiichuk
Предмет: Литература,
автор: Squirrel567
Предмет: Обществознание,
автор: 010881natasha1
Предмет: Математика,
автор: Arina28S
Предмет: Информатика,
автор: ushakovaleksey